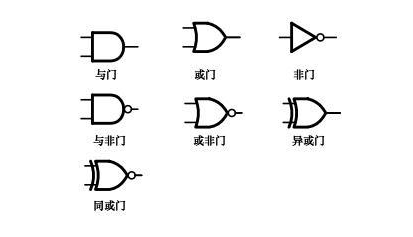
数字电路规划中逻辑门是最基本的运算单元,其间与门、或门和非门是最基本的逻辑门单元,但实践规划中用到的逻辑往往比与、或、非杂乱得多,不过它们都能够使用与、或、非门组合完成。比方与非门、或非门、异或门和同或门等等。这些逻辑门的图形符号如下图:
怎么使用门单元建立电路?
使用门单元建立的电路称为门电路,依照必定的逻辑关系使不同的门单元连接起来完成咱们所需求的逻辑功用,这便是数字电路规划的意图。下面给我们介绍两个使用逻辑门单元建立一位半加器和一位全加器门电路的比如:

上图是由一个与门和一个异或门建立的半加器电路,其间A和B是半加器的输入信号,S是半加器的成果输出,C是半加器的进位输出。
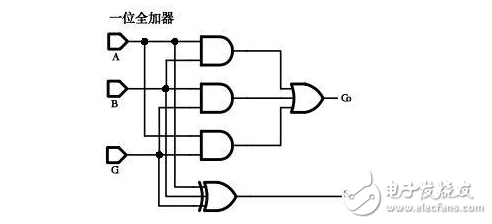
上图是由逻辑门单元建立出来的一位全加器电路,A、B是全加器的输入端信号,Ci是全加器的进位输入信号,S是全加器成果输出,Co是全加器的进位输出。
为什么能够完成加法功用?下面简略剖析一下上面两个门电路完成加法功用的原理,首要解释一下半加器和全加器的差异:半加器是只对输入信号A、B进行相加,不考虑进位;而全加器除了考虑A、B相加外还加上进位Ci。
其间,半加器相加,只要当A和B一起为1时,相加才会发生进位,因而Co=A&B。当A和B一起为0时,相加成果S=0。只要A和B其间一个为0另一个为1时,相加成果S=1,因而S=A^B。
全加器的运算杂乱一点,当A、B、Ci三个输入其间有1个或许3个都为1时,相加成果S=1,不然S=0,因而S=A^B^Ci;当A、B、Ci三个输入中恣意两个或许三个都为1时,相加就会发生进位Co=1,不然Co=0,因而Co=A&B|A&C|B&C。