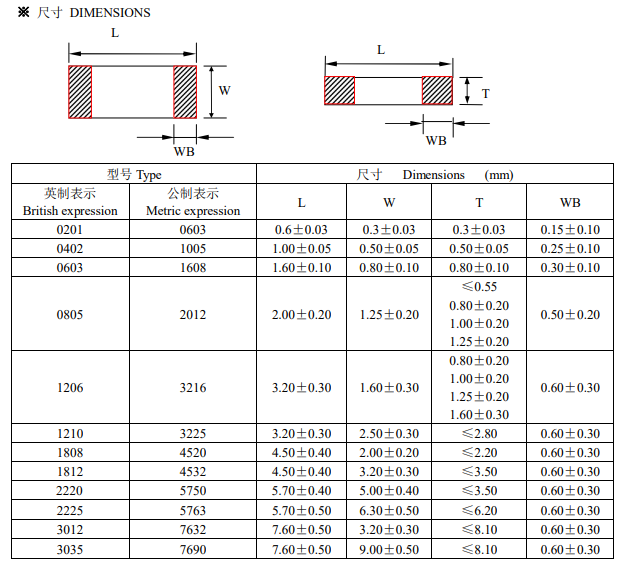
一 前置常识
拉格朗日乘子法是一种寻觅多元函数在一组束缚下的极值办法,经过引进拉格朗日乘子,可将有m个变量和n个束缚条件的最优化问题转化为具有m+n个变量的无束缚优化问题。在介绍拉格朗日乘子法之前,先扼要的介绍一些前置常识,然后就拉格朗日乘子法谈一下自己的了解。
1.梯度
梯度是一个与方向导数有关的概念,它是一个向量。在二元函数的景象,设函数f(x,y)在平面区域D内具有一阶接连偏导,则关于每一点P(x0,y0)∈D,都能够界说出一个向量:fx(x0,y0)i+fy(x0,y0)j ,称该向量为函数f(x,y)在点P(x0,y0)
的梯度。并记作grad f(x0,y0) 或许∇f(x0,y0),即 grad f(x0,y0) = ∇f(x0,y0) = fx(x0,y0)i+fy(x0,y0)j=(fx(x0,y0),fy(x0,y0)) 。
再来看看梯度和方向导数的联系:假如函数f(x,y)在P(x0,y0)点可微,el = (cosα,cosβ)是与方向L同向的单位向量,则∂f/∂L|(x0,y0) = fx(x0,y0)cosα+fy(x0,y0)cosβ = grad f(x0,y0).el = |grad f(x0,y0)|.cosθ ,其间θ表明的梯度与el 的夹角。由此可知,当θ = 0时,el 与梯度的方向相一起,此刻方向导数最大,函数f(x,y)增加最快;当θ = π时,el 与梯度的方向相反时,此刻方向导数最小且为负,函数f(x,y)减小最快。
2.等高线(等值线)
一般来说,二元函数 z = f(x,y)在几许上表明一个曲面,这个曲面被平面 z = c(c为常数)所截得的曲线L的方程为:

这是一条空间曲线,这条曲线L在xOy平面上的投影是一条平面曲线L*,它在xOy平面直角坐标系中的方程为:f(x,y) = c .关于曲线L*上的一切点,已给函数的函数值都是c,所以咱们称平面曲线L*为函数z = f(x,y)的等值线(等高线)。再来看看等高线的一些性质:
若fx,fy不一起为零,则等高线 f(x,y) = c就任一点P(x0,y0)处的一个单位法向量为:
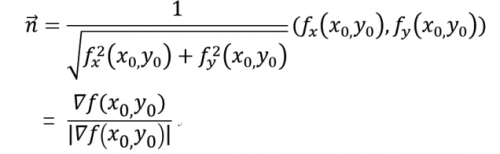
这表明函数f(x,y)在一点(x0,y0)的梯度∇f(x0,y0)的方向便是等高线f(x,y) = c在这点的法向量的方向,而梯度的模|∇f(x0,y0)|便是沿这个法线方向的方向导数∂f/∂n,所以有:
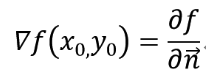
二 拉格朗日乘子法
1.等式束缚
首要看一下什么是拉格朗日乘子法,已知一个问题:
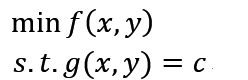
要求f(x,y)在g(x,y)=c的前提下的最小值,咱们能够结构一个函数L(λ,x,y) = f(x,y) + λ(g(x,y) – c),其间λ(λ不等于0)称为拉格朗日乘子,而函数L(λ,x)称为拉格朗日函数。经过拉格朗日函数对各个变量求导,令其为零,能够求得候选值调集,然后验证求得最优值。这便是拉格朗日乘子法。那么拉格朗日乘子法为什么是合理的?下面别离从几许和代数两方面解说下自己对其的一些见地:
(1)从几许的视点
先来看一幅图:

图中的虚线表明f(x,y)的等高线,假如满意g(x,y)=c这个束缚,必定是等高线与g(x,y)=c这条曲线的交点;假定g(x)与等高线相交,交点便是一起满意等式束缚条件和方针函数的可行域的值,但并不是最优值,由于相交意味着必定还存在其它的等高线在该条等高线的内部或许外部,使得新的等高线与方针函数的交点的值更大或许更小,只要到等高线与方针函数的曲线相切的时分,才或许获得最优值。假定该切点为P(x0,y0),则f(x,y)在p点的梯度必定垂直于其在该点处的等值线(前面现已说过),即梯度与该点出的法向量平行,又由于p点是曲线g(x,y)=c的切点,能够看做g(x,y)=c在p点处的梯度平行于它在该点的等值线的法向量,故f(x)在p点的梯度与g(x,y)=c在p点的梯度共线(由于他们在p点处的法向量是共线的),即(fx(x0,y0),fy(x0,y0)) = λ*(gx(x0,y0),gy(x0,y0))。所以最优值有必要满意:∇f(x,y) = λ* ∇(g(x)-c),λ是常数且不等于0,表明左右两头平行。这个等式便是L(λ,x)对参数别离求偏导的成果,即:
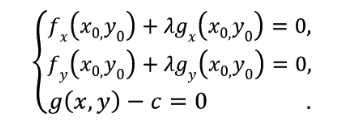
也便是说满意∇f(x,y) = λ* ∇(g(x)-c)的点必定是式子min L(λ,x) = f(x,y) + λ(g(x,y) – c)的解,所以min L(λ,x) = f(x,y) + λ(g(x,y) – c)这个式子与原问题是等价的(能够先简略的认为g(x,y) – c = 0形成的)。
(2)从代数的视点
先来看一下z = f(x,y)在条件g(x,y) = c下获得极值的必要条件。
假如z=f(x,y)在(x0.y0)处获得所求的极值,那么有 g(x0,y0) = c,假定在(x0,y0)的某一领域内f(x,y)与g(x,y) = c均有一阶段接连偏导(关于凸函数很显然是建立的)而且gy(x0,y0)≠0.由隐函数的存在定理可知方程g(x,y)=c能够确认一个接连且具有接连偏导的函数y = μ(x),将其带入z= f(x,y)中能够得到一个变量x的函数:z = f[x,μ(x)].
所以z=f(x,y)在x=x0处获得极值,相当于z = f[x,μ(x)]在x=x0处获得极值,又由一元可导函数获得极值的必要条件可知:
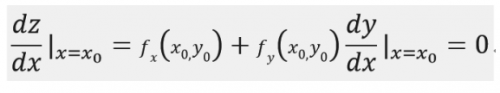
而又由y = μ(x)用隐函数求导公式,有
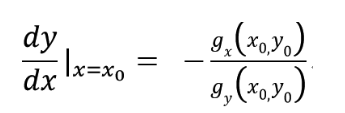
将以上两式结合可得,
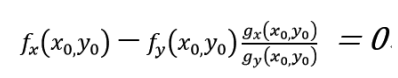
上式与g(x0,y0)=c 便是函数z=f(x,y)在g(x,y)=c的条件下获得极值的必要条件。假如令:
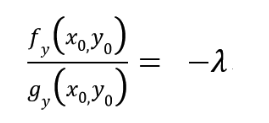
上述的必要条件就变为

同从几许视点推出的定论共同。
综上所述,关于问题

(x能够为一个矢量,也能够为一个标量)
等价于求

关于拉格朗日乘子法求出的候选值,需求留意验证;假如方针函数f(x)是凸函数的话则能够确保得到的解一定是最优解。
三 KKT条件
1.关于不等式束缚
上述问题中叙述的都是束缚条件为等式的状况,关于束缚条件为不等式的状况,一般引进KKT条件(在不等式束缚下,函数求极值的必要条件)来处理,详细如下:
关于问题

咱们也引进拉格朗日函数
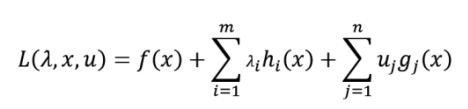
其间μj≥0。
再看一个关于x的函数:
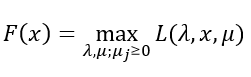
而实际上F(x)能够看做是f(x)的另一种表达方式;由于hi(x)=0,所以拉格朗日函数中的第二项为0;又由于gj(x) ≤ 0且μj ≥ 0,所以μjgj(X) ≤ 0,所以只要μjgj(X) = 0时L取到最大值;因而F(x)在满意束缚条件时便是f(x)。由此,方针函数能够表述为如下的方式:
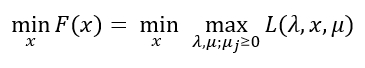
咱们称这个式子为原问题。并界说原问题的最优值为P*。
然后再看关于λ和μ的一个式子:
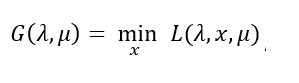
考虑该式子的极大化:
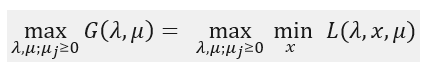
咱们称这个式子为原问题的对偶问题。并界说对偶问题的最优值为d*。
(关于拉格朗日的对偶性,可参阅李航《计算学习办法》中的附录部分,或许参阅博客:http://blog.pluskid.org/?p=702)
关于对偶性问题,一般分为弱对偶性和强对偶性:
(1)考虑到原问题和对偶问题的最优值P*和d*,假如d* ≤ P*,则称“弱对偶性”建立。
(2)假如d* = P*,则称“强对偶性”建立。
一般状况下,强对偶性并不建立;可是当原问题和对偶问题满意以下条件时,则满意强对偶性。
(1)f(x)和gj(x)是凸函数。
(2)hi(x)是仿射函数。
(3)不等式束缚gj(x)是严厉可行的,即存在x,对一切j有gj(x) < 0 。
以上三个条件也称为Slater条件。假如满意Slater条件,即原问题和对偶问题满意强对偶性,则x*和λ*、μ*别离为原问题和对偶问题的最优解的充要条件是x0和λ0、μ0满意下面的条件:

以上五个条件便是所谓的Karush-Kuhn-Tucher(KKT)条件。下面是关于这几个条件的简略论述:
关于第一个条件,由于原问题和对偶问题满意强对偶性,所以
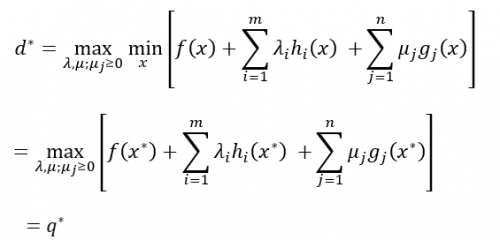
即关于x的函数:

在x*处取到了极值,由费马引理可知,该函数在x*处的偏导数为0,即:

也便是条件(1)。该式子阐明f(x)在极值点x*处的梯度是各个hi(x*)和gj(x*)的线性组合。
关于第二个条件,时在界说拉格朗日函数时的束缚条件。
关于第三个条件,在界说F(x)时就现已表现了,由于:

由于μjgj(x)≤0,要使得L最大,只要μjgj(x) = 0时满意。所以产生了第三个条件。
关于第四、五个条件,是原问题的自带的束缚条件。
当原问题和对偶问题不满意强对偶性时,KKT条件是使一组解成为最优解的必要条件,即在不等式束缚下,函数求极值的必要条件。能够把KKT条件看成是拉格朗日乘子法的泛化。