1 导言
1968年，Veselago提出了左手媒质(left-handed material – LHM)的概念, 2000年Smith等人通过周期性的排布开缝环谐振器(split-ring resonators – SRRs)和金属线(wires)初次完成了人工的LHM ，可是这种LHM结构在微波频段具有较大的损耗以及较窄的作业带宽。为了战胜这些缺陷，2002年V George等人提出了传输线型的LHM 。现在传输线型的左手媒质可以分为两类即：谐振型和非谐振型。谐振型LHM一般是通过在主传输线上周期性的加载SRR，或许对偶开缝环谐振器(complementary split ring resonator – CSRR )来组成，而非谐振型的LHM则是通过在主传输线上周期性的加载串联电容和并联电感构成 [6]。因为在频率较高时，主传输线的寄生效应将起主导作用，因而传输线型左手媒质都具有混合左右手(composite right/left- handed – CRLH)的特性。
以上这些立异的概念及结构拓宽了传统微波器材的规划思路，许多新式的微波器材如谐振器、定向耦合器、移相器、功分器和天线等都被相继提出。尤其是依据LHM的滤波器引起了研究者的广泛重视。因为LHM组元元件的亚波长特性，依据LHM的滤波器一般具有尺度小的长处，这恰能满意现代无线通信体系整机小型化的需求 。
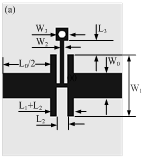
(a)物理结构
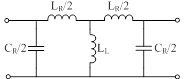
(b)集总等效电路模型
图1 新式SCRLH ZOR的
本文中提出了一种新式的简化混合左右手(simplified composite right/left-handed – SCRLH)零阶谐振器(zeroth-order resonators – ZORs)，并将其应用于小型化微带带通滤波器的规划之中。起先ZOR是规范的混合左右手(composite right/left-handed – CRLH)结构 。因为传统集总元件一般具有高频色散效应且可供挑选的元件值也是有限的，而准集总元件如交指电容的规划相对杂乱且具有较大的电尺度。考虑到这些不利因素，作者提出了SCRLH ZOR结构。本文首要给出了SCRLH ZOR的物理结构及其相应的集总等效电路模型。其次依据Bloch理论提取了谐振器的色散和Bloch阻抗特性，然后可明晰的观察到零阶谐振现象。随后选用经典的带通滤波器归纳理论以及耦合系数办法规划了三阶Chebyshev微带带通滤波器。为了满意耦合强度的要求，谐振器级间选用交指电容耦合(interdigital capacitor coupling – IDCC)结构而终端选用背槽双指平行耦合线结构(aperture-backed dual-finger parallel-coupled line structure – ADPLS)。终究依据Ansoft HFSS的仿真及优化成果制作了滤波器什物，并将实测同仿真成果进行了比较。
2 SCRLH ZOR剖析
对称SCRLH ZOR物理结构及其相应的集总等效电路模型如图1所示。ZOR由微带高/低阻抗短截线元件，接地枝节及输入输出端线构成，如图1(a)所示。与物理拓扑相应的等效电路模型如图1(b)所示，其间接地枝节等效为并联电感LL，高/低阻抗短截线以及传输端线段的总效应可由串联电感LR和并联电容CR来表征。与传统CRLH传输线元胞集总等效电路模型比较，ZOR的等效电路中移除了串联电容的部分，这将能极大的简化谐振器的规划进程。此外，在感兴趣的频率范围内，ZOR的尺度是电小的，这是
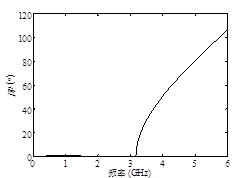
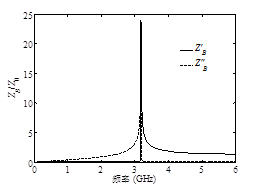
图2 SCRLH ZOR的Bloch理论剖析成果
(a) 相移特性 (b) Bloch阻抗特性
图3 终端开路的SCRLH ZOR的输入导纳特性
ZOR集总等效电路模型树立的条件。选用Ansoft HFSS进行全波仿真，ZOR的尺度为：L0 = 8.0 mm, L1 = 1.0 mm, L2 = 0.9 mm, L3 = 1.5 mm, W0 = 2.0 mm, W1 = 5.0 mm, W2 = 0.3 mm, W3 = 1.0 mm。微波介质板介电常数为2.55，损耗角正切为0.003，厚度为0.8 mm。
结合该电路模型及文献[11]中的Bloch剖析可得ZOR的零阶谐振频率为：
(1)
假定构成ZOR的两传输端线段的尺度坚持不变，则依据(1)式，可通过调整高/低阻抗短截线或许接地枝节的尺度来调谐fZOR。例如改动微带低阻线的尺度可以完成不同的CR值，但对LR和LL影响不大。相同的，改动微带高阻线或并联接地枝节的尺度可别离调整LR或LL值。依据Bloch理论剖析全波仿真S参数提取出的SCRLH ZOR的色散和Bloch阻抗特性如图2所示。从图2可知，在3.1GHz处，相移常数为零，而Bloch阻抗却非常大，这是ZOR零级谐振现象的直接证明。图3中给出了ZOR终端开路时的输入导纳特性，在3.1GHz处ZOR具有零输入导纳，这表明了ZOR具有并联谐振器的特性。
3 小型化微带带通滤波器的规划
以谐振器间耦合系数以及终端外部品质因数界说的带通滤波器网络如图4所示。设置相对带宽w = 10%，带内波纹为0.3 dB，中心频率为3.1 GHz。依据给定的目标，相应的低通滤波器原型元件值为g0 = g4 = 1, g1 = g3 = 1.371, g2 = 1.138。级间耦合系数k以及外部品质因数可表示为：
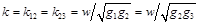(2)
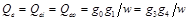(3)
因而可计算出k = 0.08，Qe = 13.70。
图4 带通滤波器网络模型
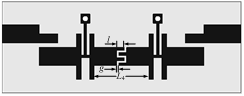
图5 谐振器级间IDCC结构
为了满意求出的级间耦合强度，谐振器间选用IDCC结构进行耦合，如图5所示。可调的参数为IDC指长l，缝隙宽度g以及相邻低阻线之间的长度L4。IDC可等效为皆为电容元件构成的П型等效电路，寄生的并联%&&&&&%效应可以通过减去一段ZOR的传输线段来消除，然后使得L4-(l+g)小于L0。耦合系数与谐振频率间的关系为：
(4)
其间fa和fb是两个IDCC谐振器在输入输出端别离选用缝隙耦合至外部端口时的传输呼应峰值对应的频率，正如图5所示。IDCC结构的优化后的参数为：l = 0.85 mm, g = 0.25 mm 及 L4 = 5.87 mm。
因为构成ZOR的传输线段的长度是固定的，为了完成所需的Qe值，滤波器的两头选用ADPLS作为端耦合结构，这样可以增强端耦合强度，ADPLS结构如图6所示。通过调整双指平行耦合线结构及地板开窗。
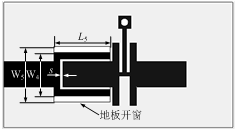
图6 ADPLS终端耦合结构
图7 滤波器什物图
结构的尺度可完成所需的Qe值。依照图6所示的结构在HFSS中树立单端口模型并求解S11，求解出频率f+ 和f–，在f+和f–处S11的相移与f0处S11相移之差别离为+90º 和-90 º，所以Qe为：
(5)
其间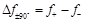
。通过全波优化可得ADPLS的尺度为：s = 0.25 mm, W4 = 3.5 mm, W5 = 4.4 mm and L5 = 4.0 mm。
归纳IDCC结构以及ADPLS的优化参数并选用LPKF S62型雕琢机制作出的滤波器什物如图7所示。随后选用了Agilent N5230A型矢量网络剖析仪对滤波器进行了丈量，仿真和丈量的传输频率呼应如图8所示。带内回波损耗的丈量值优于15dB，而带内插损在2.8dB左右。中心频率为3.1GHz的3dB带宽约为8%，扫除馈线长度，滤波器的总长度为27.0 mm。然而在3.1GHz选用相同介质板的半波长微带谐振器的长度在30.0mm以上，这意味着传统半波长谐振带通滤波器的尺度将大于90.0mm。因而与传统带通滤波器比较，选用ZOR的新式带通滤波器尺度缩减了70%以上。
4 结束语
本文提出了一种新式SCRLH ZOR结构，随后选用SCRLH ZOR作为并联谐振器并结合经典的带通滤波器规划理论以及耦合系数办法归纳出了三阶Chebyshev带通滤波器。与传统半波长带通滤波器比较，新式滤波器的尺度获得了极大的衰减，一起可以坚持杰出的传输特性。
图8 滤波器传输特性的仿真和丈量成果
