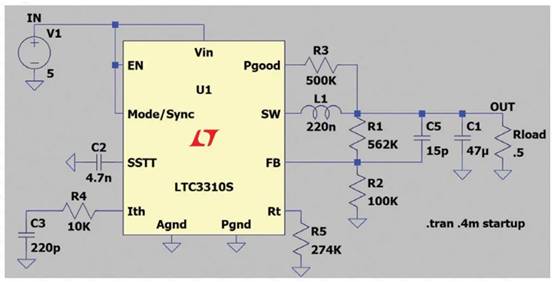
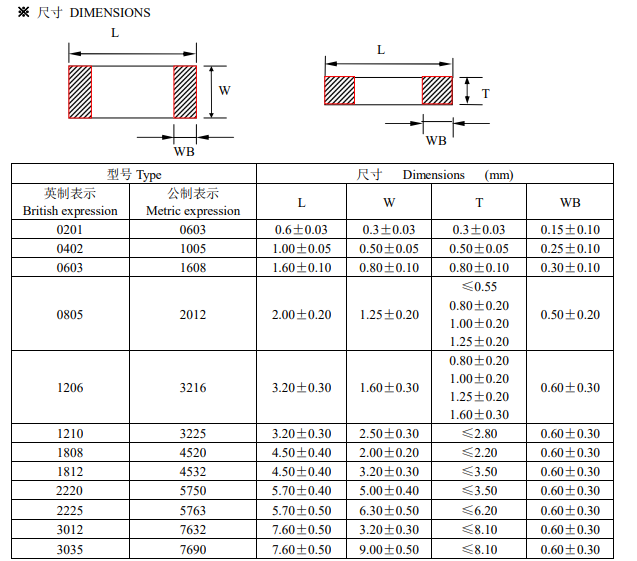
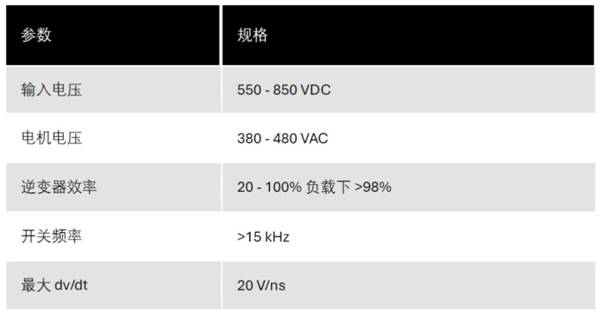
有限元法(FEM)作为一种剖析和规划东西,已广泛运用于天线、微波和信号完整性等很多电子工程范畴。FEM求解器与其它矩量法(MoM)和时域有限差分法(FDTD)等数值办法比较具有多项明显的优势。这些优势包含:能够处理杂乱的非均匀和各向异性资料、能够凭借四面体单元精确地描绘杂乱几许形状、能够运用高阶基函数完结精确性、具有多种端口和入射波等鼓励办法。运用这些功用优势,FEM就能够以极高的精确性对波导结构进行仿真。
可是,关于敞开空间问题(例如天线向敞开空间辐射的时分),FEM求解器需求经过在人工切断的鸿沟外表上设定辐射鸿沟条件(RBC),以便将无限域切断为有限域。两种广泛运用的RBC包含一阶吸收鸿沟条件(ABC)和抱负匹配层(PML),后者通常状况下都能够供给最佳的精确性。两种办法都保留了FEM体系矩阵的稀少性,但仅适用于凸起的辐射外表。两种都归于近似办法,都存在精确性问题,比方会发生来自辐射外表的非物理伪反射。这个问题能够经过增大RBC与辐射结构的间隔,让反射降至可忽视的水平,来予以处理。
另一方面,积分方程(IE)法,比方MoM,则十分适宜对坐落匀质鸿沟或无限大介质中的结构进行建模。其剖析内核选用格林函数,能够在无量远处选用Sommerfeld辐射条件。因而,不管是从内存占用,仍是从CPU时刻占用来说,对多个在空间上别离,互不相连的同质结构,IE求解器都毋庸置疑地成为更好的挑选,因为它不需求对方针之间的空间进行具体的仿真。
本文将介绍ANSYS公司在HFSS中供给的一款全新的FEBI求解器。该求解器得力于近期区域分化办法的前进。在现有的FEBI办法中,无限不知道域被分割为两个互不堆叠的域:一个有界FEM域和一个无界同质外部域。两个域间的耦合经过其接壤面上的适宜的鸿沟条件加以考虑。
依据域分化的FEBI求解器
FEBI求解器首先将原始的方针域Ω分割为两个互不堆叠的子域Ω1和Ω2,如图1所示。
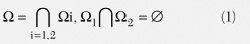

图1:将方针域分化为FEM域和IE域。Ω1和Ω2之间的公共界面在FEM域中表达为δΩ1,在IE域中表达为δΩ2。这种区别是必要的,因为现有的公式答应两个域间的非共形耦合。也就是说,能够分隔处理各个域的网格剖分、基函数和基函数阶数、矩阵树立和求解进程。关于一个稳健的FEBI求解器来说,能够以模块化的办法处理每个域的不同基函数阶数是十分重要的,因为更高阶的IE求解器还在开发的进程中。
依据上述的域分化状况,能够写出如下终究的体系矩阵:
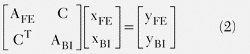
这儿,AFE和ABI别离代表FEM域和BI域的体系矩阵。C是两个域之间的耦合矩阵。由所以经过界面上的电流和磁流来完结耦合的,因而这种耦合十分稀少。等式2的解能够经过把下式拆分后迭代求得:
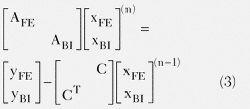
然后用迭代法求得:
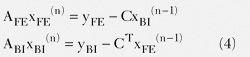
域分化法的优势能够从4式中清楚地看出。FEM域和BI域被去耦合了,因而并行化就很简单了。上文现已介绍过,BI能够在FEM顶用作精确的切断鸿沟。因为这种完结办法的模块化特征,能够轻松地完结先进的FEM求解器和IE求解器的混合求解。
运用
在本节中,将要点介绍运用这种混合办法的两个比如来突显FEBI的优势。如前文所述,一阶ABC能够用于满足大的有界共形空间,但这个空间不能有洼陷。另一方面,PML能够拉近与模型的间隔,但最适宜于长方体有界区域。对混合FEBI技能来说,因为能够精确核算鸿沟上电流和磁流的耦合,不必考虑这些外形和巨细的束缚问题。从这种新鸿沟的测验显现能够看出,当间隔为λ0/10的时分,能够完结速度和求解 规划的最佳平衡5。这儿λ0是敞开空间中的波长。别的,FEBI鸿沟能够做到彻底共形,包含凹区域。别的,还能够把模型的各个部分独立闭合为独自的域,每个域都有一个BI鸿沟。经过运用高度共形和别离空间的区域,能够大起伏缩小有限元求解域的规模,然后完结高功率的仿真。为证明这一点,下面将介绍两个比如,一个运用独立空间,一个运用高度共形鸿沟外表。
第一个比如运用的是彻底符合教科书的介质透镜6。透镜及其馈源喇叭如图2所示。透镜将来自于源天线的电磁场聚集于正前方。仿真的透镜选用长方体波导管作为馈源,其εr=2.56,正面直径为4.4λ0。然后运用混合FEBI法对体系进行别离域的建模,馈源喇叭及周围的长方体空间作为一个域,透镜周围的圆锥形区域作为另一个域,每个别离空间的切断面选用BI鸿沟。
为便于比较,一起选用了PML对该天线体系进行仿真,为求得精确的答案,运用了一个更大的长方体空气盒子将整个模型包在内,并间隔辐射体满足的间隔以确保成果的精确。与选用PML仿真比较,FEBI模型运用的较小空间能够将内存的占用下降10倍。图中一起显现了两种仿真核算得出的电场的暗影图。如其显现,尽管FEBI仿真运用的别离空间较小,透镜和喇叭表里和周边的电磁场都得到了精确的核算,并与PML核算的成果符合。喇叭的反射系数(Г)随与透镜的间隔缩小而增大。在比较加透镜前后的喇叭端口反射时,两种仿真都显现Г有1.8dB的相同增加。图3是两种办法核算得出的该天线体系的前向方向图。再度体现出FEBI和PML之间的高度符合。图2和图3阐明FEBI在运用别离空间来确认天线体系的特性时,具有适当的精确性。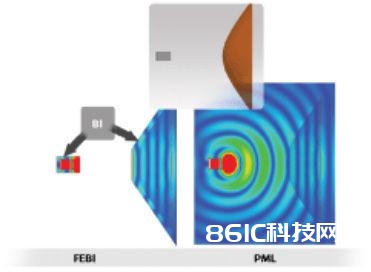
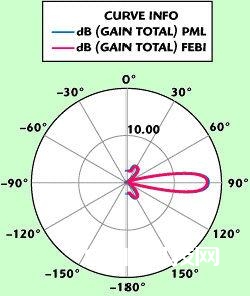
图3:透镜的辐射特性。
第二个比如考察的是一组安装在杂乱渠道上的天线阵列(图4)。它是一个由螺旋天线组成的7元阵列,安装在卫星渠道上。卫星两头之间的长度为18英 尺,天线作业频率3.5GHz。因为这是一个大型模型,所以仍是选用域分化法(DDM)来将FEM域分割为多个较小的域。7这种集成运载渠道的天线体系之前曾选用规范的ABC进行仿真,运用大型闭合长方体空间。该模型闭合的空间的体积大约为21000λ,DDM将求解规模分化为34个域。仿真一共需求的存储为210GB RAM。
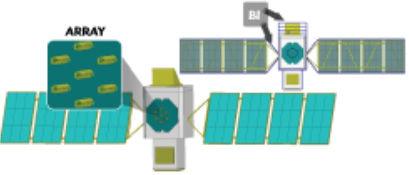
图4:安装在卫星上的螺旋天线阵列。
FEBI仿真选用全共形的空间,该共形区域如图所示。闭合的空间体积下降到1200λ3。 因为方针空间缩小,只需求在12个域上运用DDM,仿真只需21GB的RAM就满足了。相关于运用规范RBC求解,FEBI仿真所需的存储巨细会大起伏减 少。图5是两种仿真在平等起伏和相位鼓励下一切天线元的辐射特性,而两种特性完结了完美的符合。运用FEBI对坐落卫星上的等鼓励天线阵列仿真得出的三维 极坐标方向图如图6所示。依据这个比如能够了解到,经过将FEBI与高度共形的有界域结合运用,能够在单个桌面核算机上能够完结大型杂乱天线体系的仿真作业。
本文小结
混合FEBI是HFSS的FEM求解器中功用强大的新成员。规划工程师能够运用这种新技能将FEM仿真的优势与IE求解器在敞开鸿沟问题上的功率和精确性结合在一起。这个办法对共形区域、凹空间和独立空间都能获得适当的精确性,能够让用户缩小FEM求解域的规模,然后大起伏缩短求解时刻和削减求解所需占用的内存。