早在1968年,美国IBM公司的大林(Dahlin)就提出了一种不同于惯例操控规则的新式算法,即大林算法。该算法的最大特点是将希望的闭环呼应规划成一阶惯性加纯推迟,然后反过来得到能满意这种闭环呼应的操控器。
设被控目标为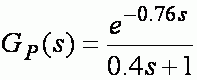
采样时刻为0.5s,用大林算法规划闭环呼应,并用MATLAB进行仿真,一起作出选用一般PID操控算法的图形,与选用大林算法的图形比较,得出结论。
参阅程序:
%Delay Control with Dalin Algorithm
clear all;
close all;
ts=0.5;
%Plant
sys1=tf([1],[0.4,1],inputdelay,0.76);
dsys1=c2d(sys1,ts,zoh);
[num1,den1]=tfdata(dsys1,v);
%Ideal closed loop
sys2=tf([1],[0.15,1],inputdelay,0.76);
dsys2=c2d(sys2,ts,zoh);
%Design Dalin controller
dsys=1/dsys1*dsys2/(1-dsys2);
[num,den]=tfdata(dsys,v);
u_1=0.0;u_2=0.0;u_3=0.0;u_4=0.0;u_5=0.0;
y_1=0.0;
error_1=0.0;error_2=0.0;error_3=0.0;
ei=0;
for k=1:1:50
time(k)=k*ts;
rin(k)=1.0; %Tracing Step Signal
yout(k)=-den1(2)*y_1+num1(2)*u_2+num1(3)*u_3;
error(k)=rin(k)-yout(k);
M=1;
if M==1 %Using Dalin Method
u(k)=(num(1)*error(k)+num(2)*error_1+num(3)*error_2+num(4)*error_3…
-den(3)*u_1-den(4)*u_2-den(5)*u_3-den(6)*u_4-den(7)*u_5)/den(2);
elseif M==2 %Using PID Method
ei=ei+error(k)*ts;
u(k)=1.0*error(k)+0.10*(error(k)-error_1)/ts+0.50*ei;
end
%———-Return of dalin parameters————
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_1=yout(k);
error_3=error_2;error_2=error_1;error_1=error(k);
end
plot(time,rin,b,time,yout,r);
xlabel(time(s));ylabel(rin,yout);

PI算法的阶跃呼应大林算法的阶跃呼应
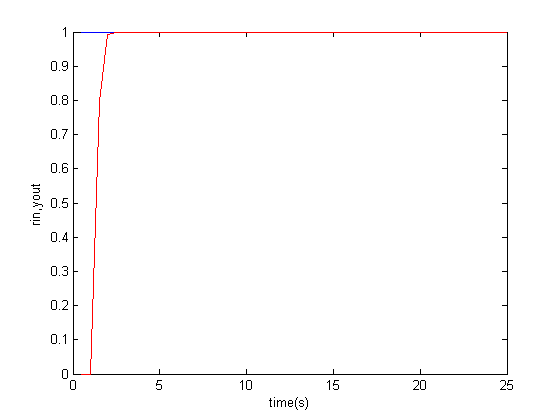
大林算法的阶跃呼应