1、导言
细长直线磁致弹性传感器是使用磁致弹性资料的磁致弹性效应完成的一种肯定式位移传感器,首要用于间隔丈量范畴,如:液位丈量、水位监测等范畴,尤其是易燃易爆、易挥发、有腐蚀的环境中[1]。
该种传感器经过检测线圈来监测磁致弹性直线上磁畴改动引起的磁通量的改动,并经过相应的时刻核算得出实测点的位移。依照引起磁通量改动的首要影响要素可将线圈检测到的电压波形分为感应波形和弹性波形两种,其间,感应波是由传感器体系驱动脉冲电流产生时,在磁致弹性线体资料上产生的周向磁场效果下,磁致弹性资料产生磁化和磁致弹性改动引起的;弹性波形是在磁致弹性效应效果下磁致弹性线体资猜中产生了的改动式超声波,当改动波抵达检测线圈方位时,磁性资料在逆磁致弹性效应下产生的[2]。
首要,感应波信号较弹性波信号强许多,相对简单检测和剖析;其次,感应波影响要素相对较少,易于给出相应的理论剖析和解说;第三,感应波产生时,磁致弹性资料产生的物理改动是产生弹性波的直接原因,对感应波的机理研讨将对研讨弹性波有着重要的含义。
作者对传感器体系中的感应波进行了多种计划的检测,剖析了感应波波形中振动产生的首要原因,对检测线圈匝数与感应波的波形信号联系进行了试验剖析和理论讨论,为该种传感器检测体系的规划及线圈参数的确认供给了理论依据和试验数据。
2、细长直线磁致传感器根本原理
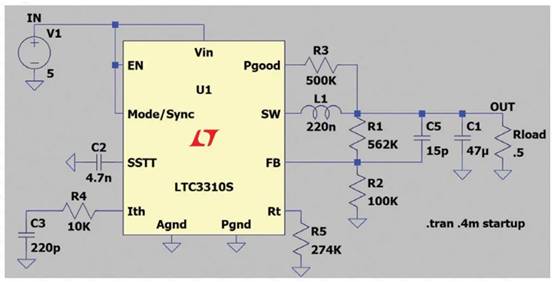
磁致弹性传感器根本作业原理如图1所示。
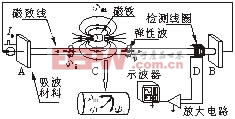
图1 磁致弹性直线传感器根本作业原理图
当给磁致弹性线加以脉冲电流Ip时,线的邻近便会产生周向磁场Фi;另一方面,在该线邻近的永久磁铁会引发轴向磁场Фm。当脉冲电流Ip流过磁致弹性线时,两磁场Фi和Фm组成一个瞬间改动磁场Ф。因为磁致弹性效应,导致组成磁场处的磁致弹性线产生瞬间形变,从而产生弹性波,并沿轴向以必定的速度v向线的两头传达。
因为磁致弹性线体资料的长度L远远大于直径D,则在核算周向磁场时可将线体假设为无限长。如图1所示,在线的一端设有检测线圈,当加载脉冲电流Ip时,载流无限长直导线周围的磁感应强度B为:
B=(μ0I)/(2πr0) (1)
在此磁场效果下,检测线圈掩盖的线体资猜中的磁畴产生偏转和磁畴壁的位移,改动了轴向磁通量的巨细,在检测线圈中便产生电压波形,在此称为感应波形。当改动波抵达检测线圈时,因为机械应力的改动,在逆磁致弹性效应的效果下,线体中的磁畴产生改动引起轴向磁通量产生改动,在线圈中产生电压波形,称为弹性波形。
依据法拉第电磁感应定律,当检测线圈轴向产生磁能量改动时,在线圈两头便产生感应电动势e,其巨细如(2)式所示。
e=-NS(B/t) (2)
式中 e:感应电压 [V];N:检测线圈的匝数;S:检测线圈金属线横截面积 [m2];B:磁通密度 [T]。因为B/t也是随时刻改动的量,所以,e是t的函数。
位移的检测是经过核算弹性波从磁铁到检测线圈之间的传达时刻t来完成的,设弹性波的传达速度为v,则永久磁铁到线圈的间隔L如(3)式所示[3]。
L=vt (3)
由图1及磁致弹性传感器原理可知,不只弹性波对检测信号有影响,并且感应波对检测信号也有影响;在实际作业体系中,影响检测信号的还应有周向磁场直接对线圈的影响、环境磁场对线圈的影响、各种环境电磁波信号对线圈的影响以及线圈及隶属检测体系电路本身的电气特性对信号的影响。
3、检测线圈与检测信号
作者选用不同匝数的检测线圈,对感应波信号进行了检测,检测线辊相关技术参数如图2所示,检测成果如图3所示。能够看出,跟着检测线圈匝数的添加,感应波振幅变大,周期变长。
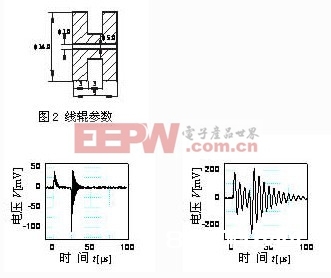
(a) 200匝 (b) 1000匝
图3 不同匝数线圈检测到的感应波形
图4为不同匝数线圈检测到的感应波形的峰峰值改动,及榜首个尖峰值的改动。
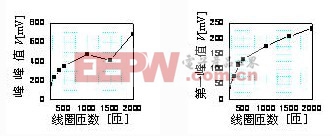
(a) 峰峰值 (b) 榜首峰值
图4 不同匝数线圈检测到的峰值
由图3和图4可知,在驱动脉冲电流的脉冲方波效果下,脉冲方波的前沿(上升沿)在线圈中产生正向的振动波形,本文称之为前沿振动;脉冲方波的后沿(下降沿)在线圈中产生负向的振动波形本文称为后沿振动,它们有以下特色:
① 感应波波形产生了两次改动,其间一次产生在驱动脉冲方波的前沿(上升沿),一次产生在后沿(下降沿);② 跟着线圈匝数的不断添加,前沿振动和后沿振动的振幅不断增大,周期也不断变长;③ 振动的影响时刻随线圈匝数的添加而变长,直到前沿振动和后沿振动交错在一起,当交错的前沿振动与后沿振动相位共同时峰峰值变大,当前沿振动与后沿振动相位相反时峰峰值变小;④由榜首峰值的改动可知,跟着线圈匝数的不断添加,榜首峰值不断变大。
本文对不同匝数线圈检测到的感应波进行了频谱剖析,随线圈匝数的改动感应波周期及频率改动如图5、图6所示。
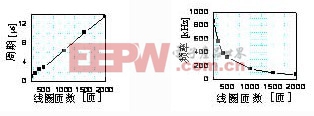
图5 线圈匝数与周期的联系 图6 线圈匝数与频率的联系
而对同匝线圈不同线体资料进行测验时,感应波主频根本共同,如表1所示。表中所示数据是选用500匝检测线圈,对六种线体资料、两种初始化计划下进行的感应波检测和主频剖析。由表可知,在线圈匝数为500匝时,所检测到的感应波形的振动频率根本保持在386kHz邻近。