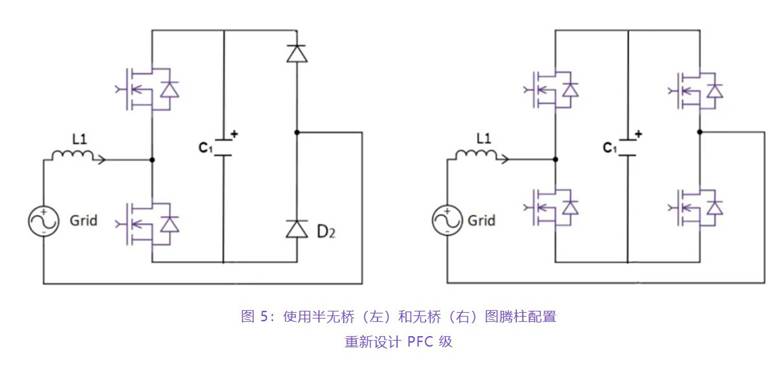
使用方程式 2 进行剖析:双极集电极散粒噪声
方程式2给出了一个双极晶体管集电极散粒噪声的联系。为了更好的了解这种联系,将其转换成一个电压噪声 Vcn(见图 7.10)能够说是好处多多。假如输入级偏置计划为已知项,则能够进行一步将公式简化。运算放大器输入级偏置计划有两类型,一类是能够迫使集电极电流与绝对温度 (PTAT) 成正比。关于一个与绝对温度成正比的偏置计划来说,集电极电流能够被视为一个常量与绝对温度的乘积。图 7.11显现了简化的 Vcn 方程式,该方程式根据一个 PTAT 偏置计划。其首要的核算结果是,噪声与温度的平方根成正比,而与 Ic 的平方根成反比。这样的核算结果阐明晰低噪声放大器总是具有强静态电流的原因。第四个经历规律便是据此得出的。该核算结果还标明,运算放大器噪声会随温度升高而增大。这便是第二个经历规律的理论基础。

图 7.10 将电流噪声转换成电压噪声

图 7.11 PTAT 偏置的集电极噪声电压
在一个集电极电流偏置不会随温度改变而产生漂移的“Zero-TC”装备中,运算放大器输入级相同会被偏置。图 7.12 显现了根据 Zero-TC偏置结构的简化的 Vcn 方程式。其首要的核算结果是,噪声与温度的平方根成正比,而与 Ic 的平方根成反比。由于受温度改变的影响很大,所以 Zero-TC 装备与 PTAT办法比较有缺乏的方面。需求留意的是,依照第二经历规律,这是最坏状况下的体现。

图 7.12 Zero-TC偏置集电极噪声电压
当 Ic 改变时,能够使用图 7.11 和图 7.12 的核算结果来确认噪声的改变量。在两种状况下,噪声均与 Ic 的平方根成反比。在一款集成电路运算放大器规划中,噪声一般首要来自差动输入级。不幸的是,产品阐明书并没有给出有关该放大器偏置的信息。为了得到一个大约的预算值,您能够假定 Ic 的改变是与静态电流 (Iq) 的改变成正比例的。总归,输入级偏置要比 Iq 更好操控,因而这是一个保存的预算值。图 7.13 显现了一款 OPA227 在最坏状况下的噪声预算值。需求留意的是,在此状况下,Iq 的改变对噪声几乎没有影响。就大部分实践规划而言,这种改变不会超越 10%。请留意,热噪声变量和散粒噪声变量(Ic 变量)均不大于 10% 是第一个经历规律的理论基础。

图 7.13 根据 Iq 变量的最坏状况噪声
使用方程式 3 进行剖析:双极基极散粒噪声和闪耀噪声
方程式 3 描绘的是双极晶体管基极散粒噪声和闪耀噪声,该噪声源与运算放大器中的电流噪声相类似。也能够将该电流噪声转换成电压噪声(请参见图 7.14)。对 PTAT 和 Zero-TC 偏置结构进行剖析,可不像对集电极电流散粒噪声进行剖析那么简略。这是由于偏置办法是为了对集电极电流进行操控而规划的,而且此种相关不会跟从基极电流。例如,一款带有 Zero-TC 集电器电流的器材不会有 Zero-TC 基极电流,由于双极电流增益随温度的改变而改变。
方程式 3 中的散粒噪声重量是形成宽带电流噪声的首要原因。请留意,电流噪声与 Ib 的平方根成正比,这便是宽带电流噪声要比宽带电压噪声更简单受影响的原因地点。Ib 的改变是由晶体管的电流增益 (beta) 形成的。
请留意,散粒噪声重量的方式与方程式 2 中的噪声重量方式相同。因而,除很难估计基极电流的温度系数以外,其他剖析办法是相同的。所以为了简化起见,咱们将不会把 Ib 散粒噪声的温度信息包含在内。
如图 7.14 所示,咱们能够将闪耀噪声重量转换成一个电压噪声。请留意,闪耀噪声随温度的升高而增大,并随 Ic 的改变而下降。但是,闪耀噪声极易受工艺改变的影响,以至于闪耀噪声常量的改变或许会成为噪声的首要来历。这不同于常量不受工艺改变影响的宽带状况。第二个经历规律便是根据这个根本联系得出的。

图 7.14 闪耀噪声电压联系
FET 噪声具体的数学核算办法
图 7.15 为 MOSFET 和 JFET 晶体管噪声模型示意图。图 7.16(方程式 4 和 5)给出了 FET 晶体管的根本噪声联系。在这一节里,咱们将使用这些方程式来阐明该经历规律也相同适用于 FET 晶体管。图 7.17 为处理过的热噪声方程式,该方程式用于强反相 (strong inversion) FET 的 PTAT 和 Zero-TC 偏置。强反相是指 FET 偏置区。强反相的核算结果为热噪声与 Id 的四次方根成反比。热噪声与绝对温度的平方根成正比仍是与绝对温度的四次方根成正比取决于偏置类型。因而,与双极放大器比较,Iq 或温度上的改变对强反相 FET 放大器的影响要小得多。
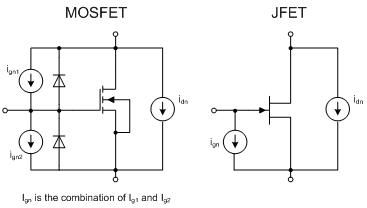
图 7.15 双极晶体管噪声模型

图 7.16 根本 FET 噪声联系

图 7.17 强反相 FET
图 7.18 给出了将一个热噪声方程式用于弱反相 FET 的 PTAT 和 Zero-TC 偏置的操作。弱反相是指 FET 偏置区。弱反相的核算结果为热噪声与 Id 的平方根成反比。热噪声与温度成正比仍是与温度的平方根成正比取决于偏置类型。因而,弱反相 FET 放大器和电流及温度的联系与双极偏置放大器和电流及温度的联系类似。
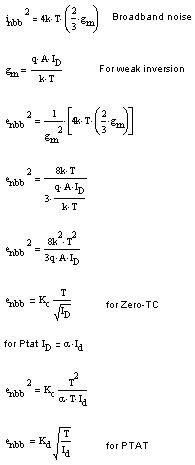
图 7.18 弱反相 FET
图 7.19为处理过的闪耀噪声方程式,该方程式用于强反相 FET 的 PTAT 和 Zero-TC 偏置。请留意,方程式中的“a”为介于 0.5 和 2 之间的一个常数。因而,闪耀噪声或许和 Id 成正比,或许和 Id 的幂成反比,这取决于“a”的值。关于一款 Zero-TC 偏置计划来说,闪耀噪声的值并不取决于温度。关于一款 PTAT 偏置计划来说,闪耀噪声和温度的平方根成正比。
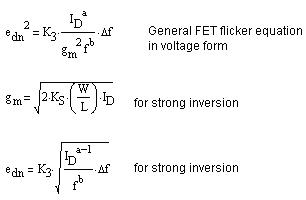
图 7.19 强反相 FET 闪耀噪声
图 7.20 显现了用于核算一个弱反相 FET 的 PTAT 和 Zero-TC 偏置的闪耀噪声方程式。请留意,“a”是一个介于 0.5 至 2 之间的常数。因而,在所有状况下,闪耀噪声都与 Id 的幂成反比。就一个 Zero-TC 偏置而言,闪耀噪声将会与绝对温度成正比;就一个 PTAT 偏置而言,温度联系则取决于 a 的值。
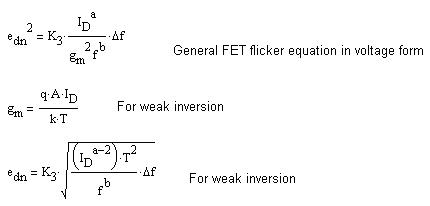
图 7.20 弱反相 FET 闪耀噪声
总结与概述
本文中,咱们评论了一些有助于咱们对最坏状况下的噪声和与温度相关的噪声进行预算的经历规律。这此经历规律还能够协助那些电路板和体系级规划人员取得折衷规划的办法,而这些办法正是集成电路规划人员在低噪规划中所选用的。一起,还给出了这些经历规律背面的具体数学核算办法。第 8 部分将首要对 1/f 噪声及“爆米花”噪声进行更深化的讨论。
感谢
特别感谢 TI 的技能人员,感谢他们在技能方面所供给的真知灼见。这些技能人员包含:
- 高档模仿 %&&&&&% 规划司理 Rod Bert
- 线性产品司理 Bruce Trump
- 使用工程司理 Tim Green
- 高速产品商场开发司理 Michael Steffes
参考书目
《模仿%&&&&&%的剖析与规划》,作者:Paul R. Gray 与 Robert G. Meyer,第三版,由 Hamilton Printing Company 出书。