收到QQ上一个留言,有位网友问询我一个简略的问题。问题如下:
1111 011. 1 0001 1110 1011 1000=123.559998,小数点后是怎样核算的呢?谢谢您!
很明显1111 011. 1 0001 1110 1011 1000是一个二进制数。整数部分当然好核算,将每位的权值加起来即可。这位网友问询的是小数部分的核算方法。其实也十分简略。
0.10001111010111000=2^(-1)+2^(-5)+2^(-6)+2^(-7)+2^(-8)+2^(-10)+2^(-12)+2^(-13)+2^(-14)=0.559998
这个能够经过核算器来核算。可是小数后位数太多,简略犯错。咱们能够编写一段简略的代码来核算。代码如下:
#include
#include
char a[]="10001111010111000";
void main( )
{
unsigned char i;
double sum =0.0;
printf("sum=");
for( i =0 ; i< sizeof(a); i++)
{
if( a[i] ==’1′)
{
sum = sum + pow(2,-(i+1));
printf("+2^(%d)",-(i+1));
}
}
printf("\n%f\n", sum);
}
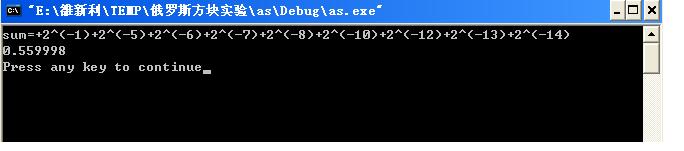
我这样答复期望他理解!