拉普拉斯改换是工程数学中常用的一种积分改换,又叫拉氏改换。拉氏改换是一个线性改换,可将一个有引数实数t(t≥ 0)的函数转换为一个引数为复数s的函数。拉氏改换英文名为Laplace Transform,为法国闻名数学家拉普拉斯(Laplace,Pierre-Simon,marquisde)创建。首要运用于现代操控范畴,和傅氏改换并称为操控理论中的两大改换。
拉氏改换里的S是复变函数里最为根底的一个符号,数学题做了这么多,考分也不低,但假如在多年的电路设计中用不上的话,岂不是对不住名贵的芳华了。
要用好拉氏改换,先了解S的物理意义和其用处。信号剖析有时域剖析、频域剖析两种,时域是指时刻改变时,信号的幅值和相位随时刻改变的联系;频域则是指频率改变时,信号的幅值和相位随时刻改变的联系;而S则是衔接时域与频域剖析的一座桥梁。
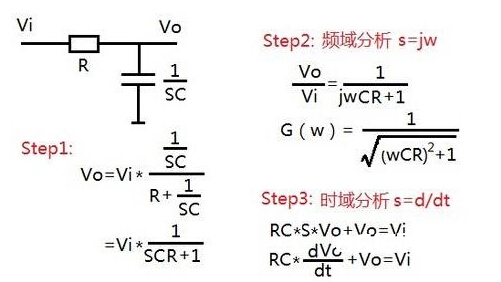
在电路中,用到的阻性用R表明;用到的理性特性和容性特性,分别用SL和1/SC表明,然后将其当作一个朴实的电阻,只不过其阻值为SL(电感)和1/SC(电容);
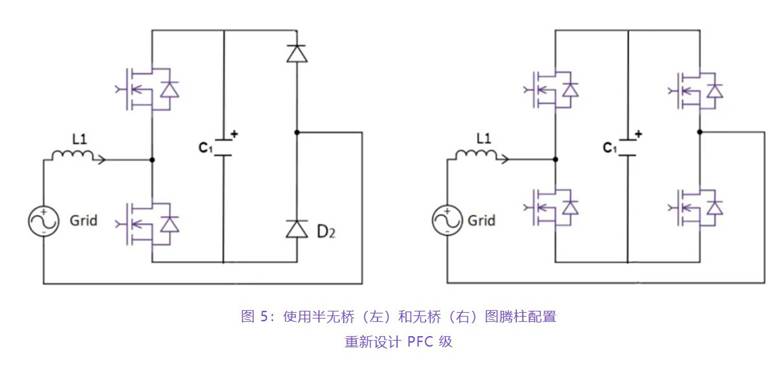
其他特性(如开关特性)则均可经过画出等效电路的方法,将一个杂乱的特性分解成一系列阻性、理性、容性相结合的方法。并将其间的理性和容性分别用SL和1/SC表明。
然后,就可以用初中学过的电阻串、并联阻抗核算的方法来进行分压、分流的核算,这当然很简略了。核算完后,最终必定会成一个如下四种之一的函数:
Vo=Vi(s)——————–(1)
Io=Vi(s)——————–(2)
Vo=Ii(s)——————–(3)
Io=Ii(s) ——————–(4)
下一步,假如是做时域剖析,则将S=d/dt代入上述1-4其间之一的式子中,随后做微分方程的求解,则可求出其增益对时刻的改变式 G(t);
而假如做的是频域剖析,则将S=jw代入上述1-4其间之一的式子中,随后做复变函数方程的求解,则可求出其增益对时刻的改变式 G(w)、和相位对频率的改变式 θ(w);
至于求出来时域和频域的特性之后,您再想把数据用于什么用处,那就不是我能关怀得了的了。
下面举一简略比如阐明。