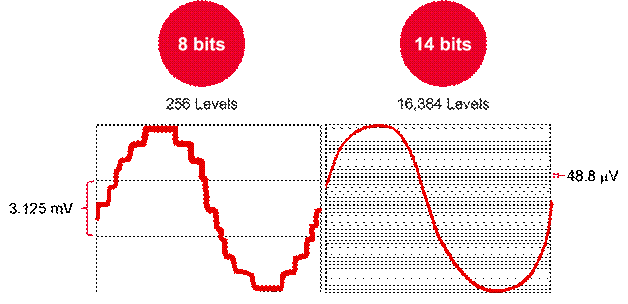
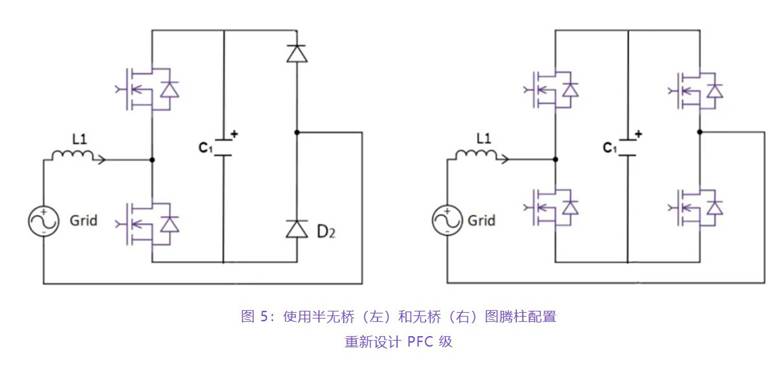
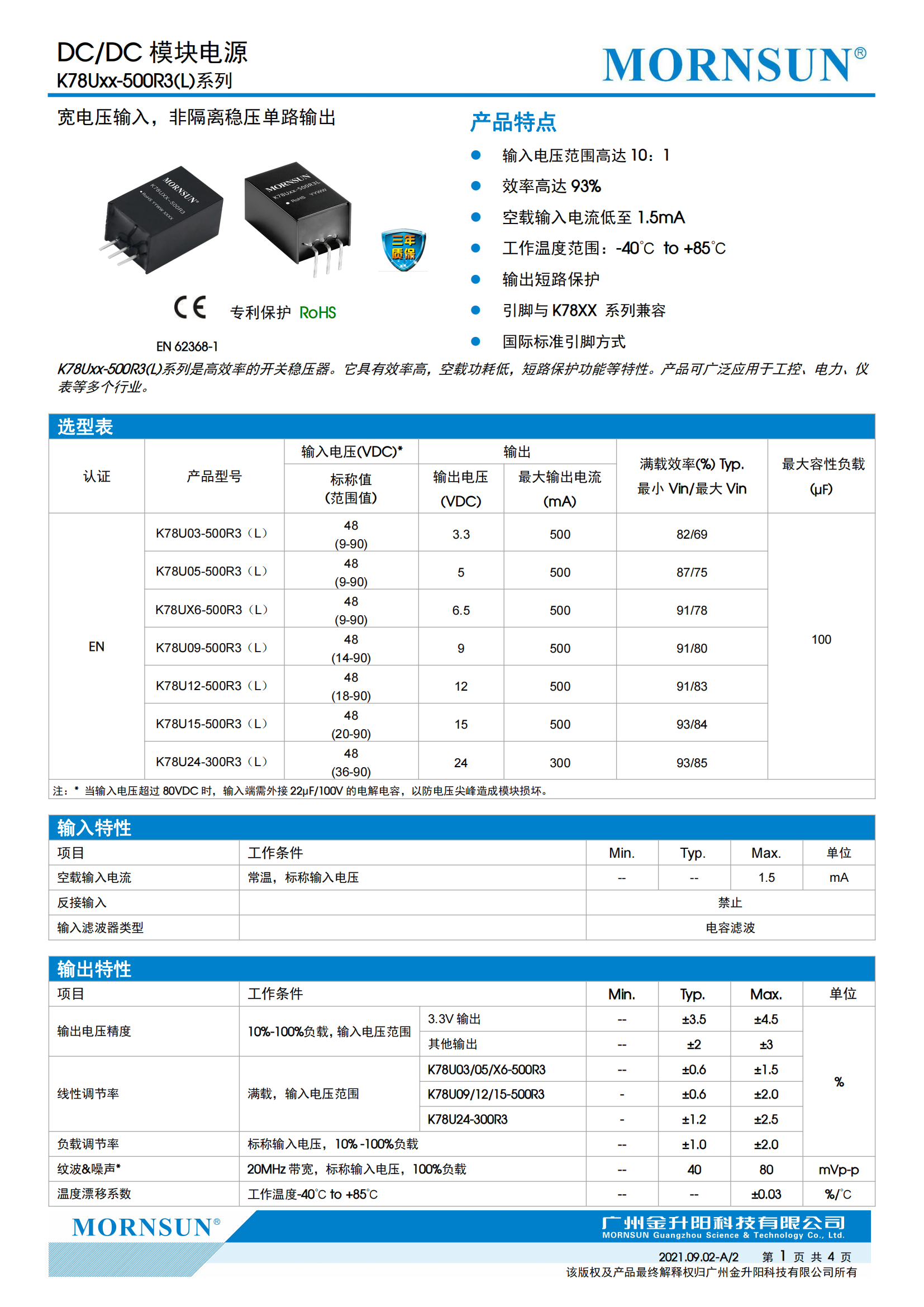
LED光源的最大特色便是寿数长,可到达50000~100000小时,长期的监测其光衰状况是不实际的,因而,本规范将通过一种加快寿数实验的办法来猜测LED照明灯具的寿数。
适用范围
本规范适用于各类LED照明灯具的寿数测验,不包括灯具的电源部分的测验。
技能要求
把LED灯具的光输出为初始光输出的70%作为寿数判别失效的目标。
实验办法一
结温是影响LED光衰减的重要原因。结温的升高会使LED光衰很快。LED在高电流下作业会发生更多得热量,然后加快老化。
本实验办法选用不同的驱动电流,选取5只LED灯具,在25℃环境温度下,用不同电流进行加快寿数实验,得出光输出衰减的数学模型。
数学模型
y=exp(-αt)
α=m×exp(nI)
其间y表明相对光输出,α表明衰减常数,t为点灯时刻,m、n为常数,I为测验电流。
依据不同电流下的得到的关于y和t的测验数据,终究得出关于不同灯具的衰减系数α,然后得出光通保持率在70%的寿数值t70%
实验办法二
选用温度作为稳定的加快应力,计算出在25℃下LED灯具失效判据70%时的希望寿数。
选取5个相同标准的LED灯具,调理烘箱的温度,分别在50℃、80℃、100℃、120℃、150℃ 条件下,在额定电流、恒流条件作为稳定加快的条件。
记载5组LED可靠性实验进程的一切参数:光输出(照度或光强或光通量)、实验时刻、电流、功率、结温等。
选用阿仑尼斯数学模型
P=P0exp(-βt)
β=β0IFexp(-Ea/kTj)
其间P0为初始光输出,P为加温加电t时刻后的光输出,β为某一温度下的衰减系数,t为某一温度下的加电作业时刻,β0为常数,Ea为激活能,k为波尔兹曼常数,IF为作业电流,Tj为结温。
通过公式改换和实验数据得出
Ea=[K×In(t2/t1)]/(1/Tj2-1/Tj1)
t2=t1×exp[Ea/K(1/Tj2-1/Tj1)
然后得出25℃下失效判别为70%的预期寿数。