奈奎斯特采样定理,或许更准确地说是奈奎斯特-香农定理,是操控混合信号电子体系规划的根本理论原理。
正如咱们所知道的,假如没有模数转化和数模转化,现代技能就不会存在。实际上,这些操作现已变得十分遍及了,以至于说“一个模仿信号能够转化成数字信号,然后再转化成模仿信号,而不会形成任何严峻的信息丢掉”。
这听起来像是一种真理,但咱们怎样知道状况的确如此呢?当它看起来好像丢掉了咱们在单个样本之间调查到的如此之多的信号行为时,为什么还说采样是一种无损操作呢?
如图1所示,咱们怎样能从一个这样的信号开端:
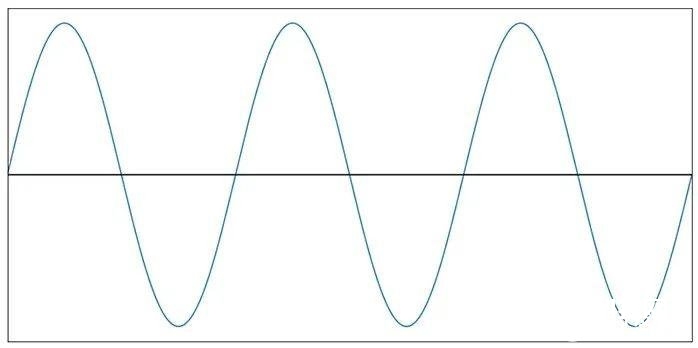
图1
再将其数字化成图2这样:
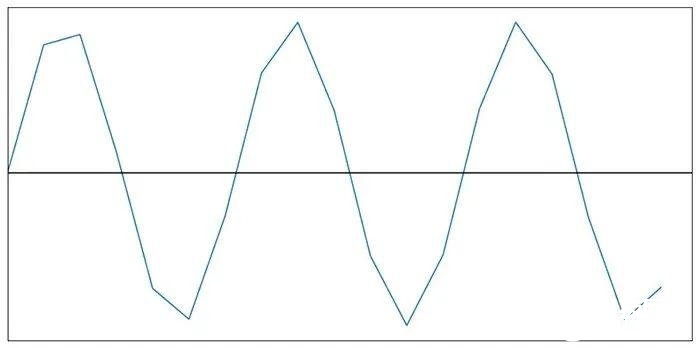
图2
然后还敢宣称“原始信号能够康复,且不会丢掉信息”?
奈奎斯特-香农定理
之所以能够提出这样的说法,是因为它契合现代电气工程最重要的原理之一:
假如一个体系以超越信号最高频率至少两倍的速率对模仿信号进行均匀采样,那么原始模仿信号就能从采样发生的离散值中彻底康复。
关于这个定理还有很多话要说,但首要,让咱们试着弄清楚究竟该怎样称号它。
香农?奈奎斯特?科捷利尼科夫?惠特克?
我当然不是那个决议谁在论述、证明,或许解说“香农-奈奎斯特-科特尔尼科夫-惠特克”采样和插值理论方面最值得赞扬的人。其实,这四个人都有参加其间,而且取得了显着成效。
但其间,哈里 · 奈奎斯特这个人的人物,好像现已超出了它开始的含义。例如,在谭和江编撰的《数字信号处理:根本原理与运用》一书中,上述原理被确定为“香农采样定理” ;在塞德拉和史密斯的《微电子电路》一书中,我发现了下面这句话:“事实上,咱们能够在有限数量的样本上进行处理……而疏忽样本之间的模仿信号细节……这是根据香农采样定理。”
因而,咱们或许应该防止运用“奈奎斯特采样定理”或许“奈奎斯特采样理论”这些词汇。假如咱们需求把姓名和这个概念联系起来,那么我主张只含有“香农”或许“奈奎斯特和香农”。事实上,也许是时分过渡到更匿名的东西了,比方“根本采样定理”。
假如你觉得这有点令人利诱,请记住上面说到的采样定理与奈奎斯特速率是不同的,本文稍后将对此进行解说。我以为,没人能把奈奎斯特和他的速率分隔,所以终究达成了一个很好的退让:香农得到了定理,奈奎斯特得到了速率。
时域采样定理
假如咱们将采样定理运用于频率f信号的正弦波,就必须要对f样本≥2f信号的波形进行采样才干完成完美重构。换句话说,每个正弦周期至少需求两个样本。接下来,让咱们先从时域的视点来了解一下这句话。
在下面这张图中,正弦波的采样频率远远高于信号频率:
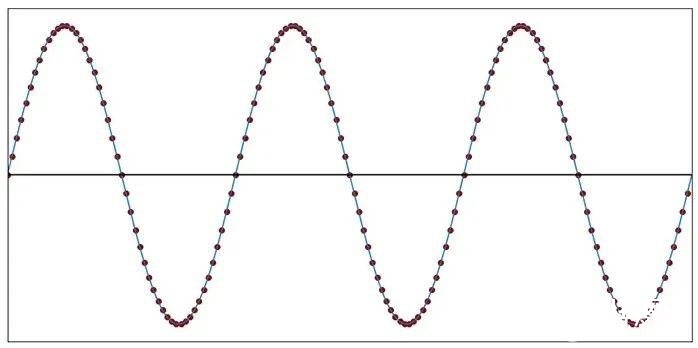
图3:每个圆点代表一个采样瞬间,即丈量模仿电压后,并将其转化为数字的准确时刻
为了愈加直观地了解这个采样进程,咱们能够制作采样值,然后用直线将它们连接起来。如下图所示的直线近似值看起来与原始信号彻底相同:相较于信号频率,采样频率十分高,因而线段与相应的曲线正弦波线段没有显着的差异。
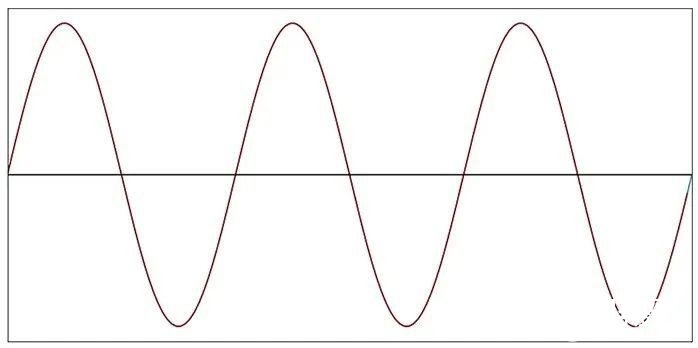
图4
但跟着咱们下降采样频率,直线近似值的外观与原始图画有所不同了。
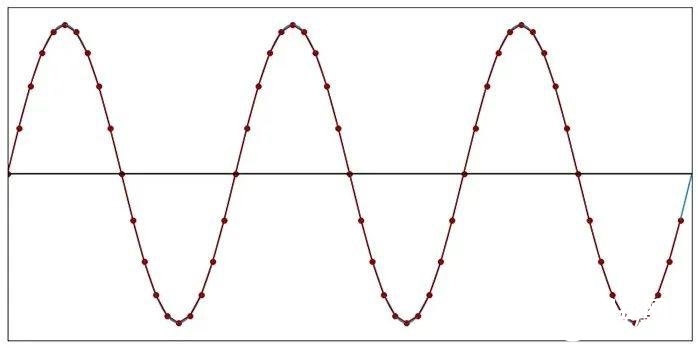
图5:每个周期20个样本(f样本=20f信号)
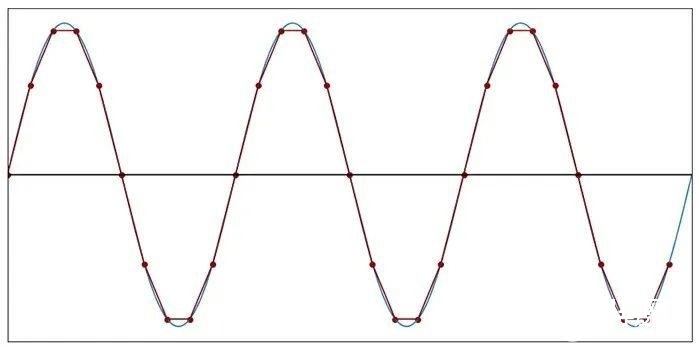
图6:每个周期10个样本(f样本=10f信号)
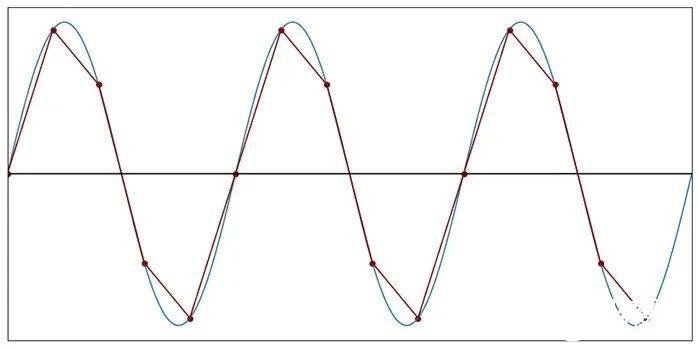
图7:每个周期5个样本(f样本=5f信号)
临界值:每个周期2个样本
跟着咱们把每个周期的采样数量削减到5个以下,采样发生的数据点仍将持续坚持模仿信号的循环性质,但终究会到达一个频率信息被损坏的点。首要,考虑下面的情节:
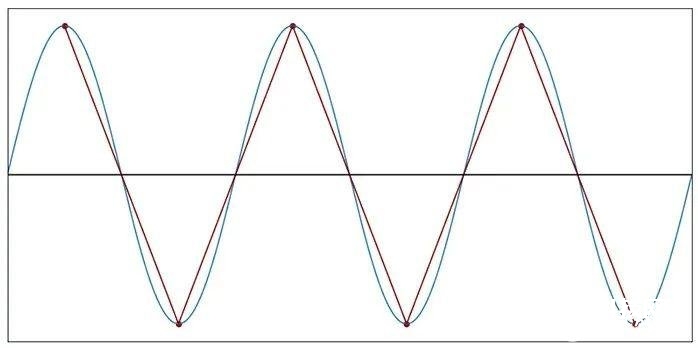
图8:每个周期2个样本(f样本=2f信号)
当f样本=2f信号时,正弦曲线彻底消失了。可是,由采样数据点发生的三角波并没有改动正弦曲线的根本周期性,三角波的频率与原始信号的频率相同。
但是,一旦咱们将采样频率下降到每个周期少于2个样本时,这种说法就不再成立了。因而,在混合信号体系中,关于原始信号中的最高频率,每个周期2次采样是至关重要的临界值,其对应的采样频率就称为奈奎斯特速率:
假如咱们以低于奈奎斯特速率的频率对模仿信号进行采样,那么将无法完美地重构原始信号。
下面两张图显现了当采样频率低于奈奎斯特速率时所发生的周期性等效丢掉:
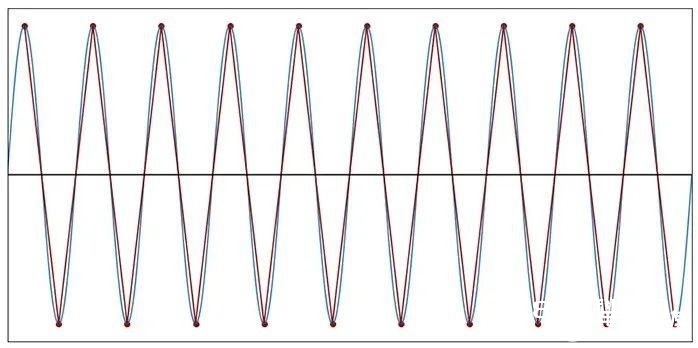
图9:每个周期2个样本(f样本=2f信号)
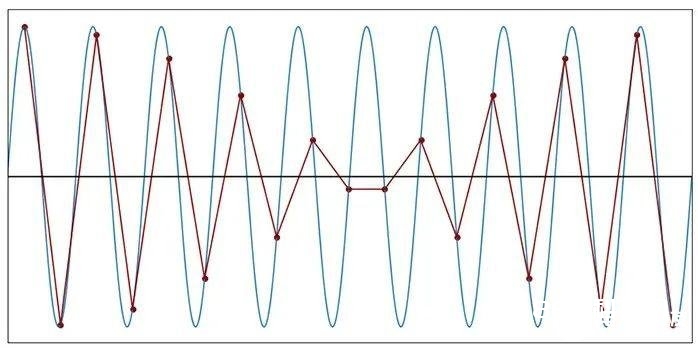
图10:每个周期1.9个样本(f样本=1.9f信号)
当f样本=1.9f信号时,离散时刻波形根本上获得了全新的周期性行为。采样形式的彻底重复,需求一个以上的正弦波周期。
但是,当咱们每个周期只要1.9个样本时,采样频率缺乏的影响就有点难以解说了。接下来的情节,更清楚地说明晰这一切:
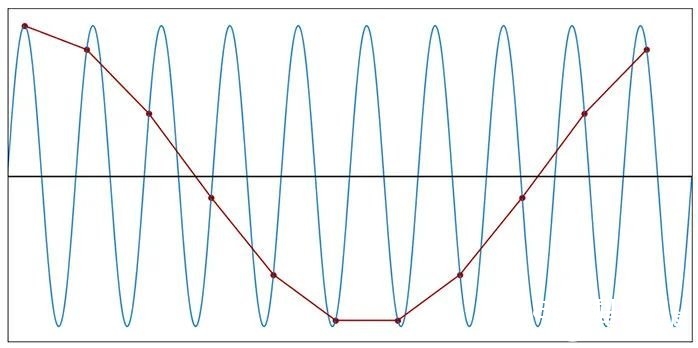
图11:每个周期1.1个样本(f 样本 =1.1f 信号 )
假如你对正弦波一窍不通,而且运用1.1f信号采样发生的离散时刻波形进行剖析,那么你将会对原始信号的频率发生严峻的错误想法。此外,假如你只要离散数据,那么就不或许知道频率特性现已被损坏了。采样发生了一个原始信号中不存在的新频率,但你不知道这个频率不存在。
所以,终究结论是:当咱们以低于奈奎斯特速率的频率采样时,信息就会永久地丢掉,原始信号无法完美地重构。
结语
本文评论了香农采样定理和奈奎斯特速率,而且企图经过调查采样在时域中的影响来深化了解这些概念。