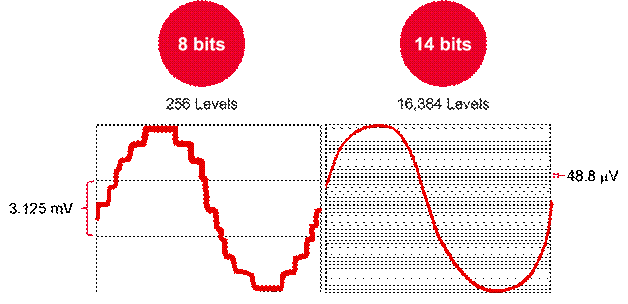
在做滤波器、扩大器
或许EQ电路设计时，一般需求重视频率与强度的联系，这便是波特图。滤波器、扩大器的波特图一般有两部分组成：幅频特性图和相频特性图，这两种图从不同的视点描绘滤波电路的特性。在我接触到的EQ电路中，只重视幅频特性联系。幅频特性图中横坐标为频率，单位为Hz，纵坐标为对数联系，一般用分贝(dB)表明，核算联系为20log(Au)。一个典型的波特图如下图所示：
在一些书本的描绘中，常常会呈现dB/2倍频、dB/6倍频和dB/10倍频，这都是为了更好的描绘幅频特性联系而引进的描绘。现在咱们先以dB/2倍频为例进行具体阐明。
首先从数学的视点来剖析该单位的含义：纵坐标dB每添加1的dB横坐标频率即将添加2倍，严厉含义上来说是以2倍频率的速度来进行纵坐标强度的判别，这样一来，比用1倍频率的横坐标改变量有更快的描绘。从电子学方面看，选用2倍频作为标准时，虽然在-3dB方位的频率承认有了必定的含糊，可是，能够从幅频特性图中愈加精确的得出在2倍频处的起伏特性。相同，dB/6倍频和dB/10倍频也是这个道理。
进一步，在滤波器和运放电路设计中，常常用到-3dB/倍频、-6dB/2倍频和-20dB/10倍频来描绘电路特性，现在解说下为什么选用这样的描绘。
-3dB/倍频:20log(Au)=-3 Au=0.707 也便是说频率添加1倍，起伏降低到本来的0.707
-6dB/2倍频:20log(Au)=-6 Au=1/2 也便是说频率添加2倍，起伏降低到本来的1/2
其他数值的分贝倍频联系能够同过以上公式进行核算，一般这么做都是为了便利频率得出扩大倍数与频率的联系。
这些描绘在数学视点来说有出力不讨好的预兆，可是，在电子学方面，却很形象的描绘出了要害频率点和起伏之间的联系。
咱们了解了不同倍频之间的含义之后，下一步在来剖析核算下不同单位倍频之间的联系，现在咱们以-3dB/倍频和-20dB/10倍频为例进行核算。这其实便是朴实的数学改换，也趁便阐明晰一个道理，数学学科深化、进入到了社会学科的不同范畴。
在-3dB/倍频中，假如其波特图改变如下：
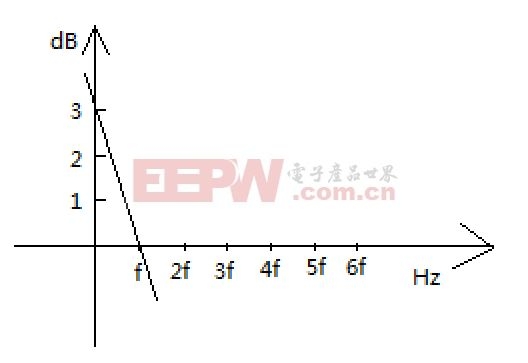
从数学视点来了解剖析-3dB/倍频，根据上图来看，横坐标为倍频，纵坐标为强度dB，用数学的表达式为
y=-3x+1(该式子很好的描绘了频率每添加一倍，强度减小3)
那么当横坐标为10倍频的时分，其波特图如下所示
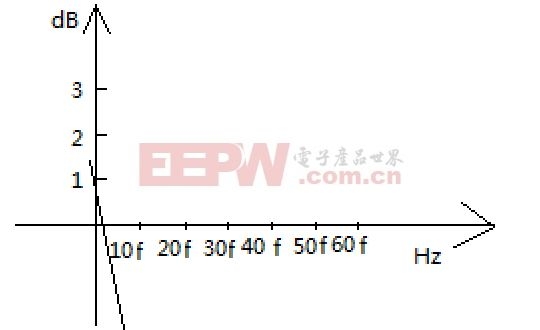
用数学表达式表明上图的数学联系为
y=-28x+1(该式子表明为横坐标以10倍频率添加，每添加一倍，强度减小28dB)
这样，从数学视点清晰了不同倍频下强度的改换联系，使不同的强度改变(斜率)体现的愈加显着。
还有别的一种方式，特别是在波特图奇零点剖析时，由于幅频特性曲线每通过一个零点斜率就会减小一倍，每通过一个极点就会增大一倍，所以会在幅频特性曲线中见到-10dB/10倍频、-20dB/10倍频的斜率。
通过以上的数学剖析，咱们了解了不同分贝每倍频之间联系，这样，在今后碰到不同数值和不同分贝每倍频时，不能从数值上表明巨细，只要改换为相同倍频的时分才干比较巨细，这点有必要要注意。
