FFT作为数字信号处理中的重要的手法之一，首要在数字通信、语音信号处理、图画处理、功率谱估计、仿真、系统剖析、雷达理论、光学、医学、地震以及数值剖析等方面得到广泛应用。根据FPGA完结FFT，具有软件编程的灵活性及电路扩展性强等长处。跟着集成电路技术进步和制作工艺水平的进步，FPGA芯片具有的功用越来越强，成为快速实时完结FFT的重要手法。选用基2法完结根据FPGA浮点运算器的FFT。
1 根据FPGA浮点运算器的FFT
1．1 浮点的IEEE规范格局
规划选用单精度浮点运算，IEEE界说的二进制浮点格局为32位。结构标明如图1所示。
将32位分为3部分：31位为符号位S，S为0时标明正数，为1时标明负数；30～23为指数E，是一个0～255之间的八位二进制数，其实践的指数是E-127，所标明的指数规模是2-127～2128；22～0标明尾数F，小数点前还躲藏了一位‘1’，单精度尾数可标明最大数为2(23+1)=16 777 216。由于10716 777 216108，所以单精度浮点数的有效位数是7位，即浮点数的精度为10-6。为便利FFT的运算，文中选用原码存储。
1．2 基2的DIT-FFT算法
在蝶形运算中选用复数方式标明数据。关于一个2点的蝶形运算，输入复数为A=x+jX，B=y+jY；经
运算，输出复数A’=(x+ycosφ+ Ysinφ)+j(X+Ycosφ-ysinφ)，B’=[x-(ycosφ+Ysinφ)]+j[X-(Ycosφ-ysinφ)]。
规划首要针对8点FFT进行规划，8点FFT算法的原理图如图2所示。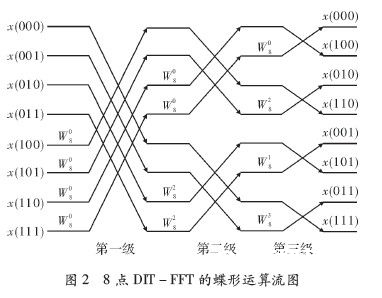
整个FFT进程中共有三级蝶形运算，每级蝶形运算有4个蝶形运算单元。在数据输入时依照天然次序输入，最终倒序输出。
1．3 FFT处理器
FFT处理器首要对数据进行蝶形运算及数据存取。规划选用基2蝶形运算器，包含存储器ROM和RAM，操控器及地址发生单元等。其FFT的结构模型如图3所示。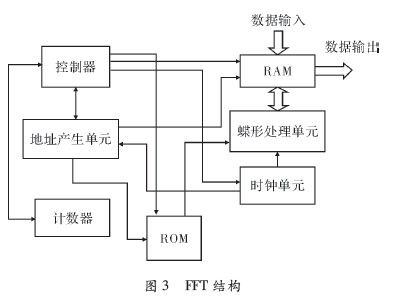
1．3．1 蝶形处理单元
蝶形处理单元是整个FFT的中心环节，选用复数标明，将实部与虚部别离存储，使用基2的DIT-FFT算法完结运算。
蝶形运算进程包含一个乘法运算和一个加／减法运算。数据的读取由时钟单元的信号来操控：当时钟为c0时，读取y；c1时，读取Y；c2时，读取x；c3时，读取X。经蝶形运算后得到x’=x+(ycosφ+Ysinφ)，X’=X+(Ycosφ-ysinφ)，y’=x-(ycosφ+Ysinφ)，Y’=X-(Ycosφ-ysinφ)然后将数据写入相同地址的RAM中，至此，2点的蝶形运算单元完结。在蝶形运算共需一个乘法器和两个加法器。
(1)浮点乘法器。乘法进程对浮点数的符号位、指数以及尾数别离进行核算，符号异或，指数相加再减127，尾数参与隐含的‘1’后再进行乘法运算，假如尾数相乘的成果有溢出则指数加1尾数取前23位，若无溢出，则取最高位后的23位。但若输入的数据有一个是0，则输出为0。
图5的波形为两浮点数的乘法运算，输入以16进制标明，别离将不同类型的数据分配进行测验，成果标明仿真正确。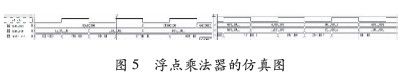
(2)浮点加法器。加法运算是将两数指数比较，存储较大的指数，将指数小的尾数移位，再进行加减操作，规格化后输出。加法进程由多个模块组合完结，包含比较模块，右移模块、加／减法模块、前导零检测模块、左移模块和成果整合输出模块。
比较模块首要对指数操作，判别指数的巨细，较大的指数暂作成果的指数，较小指数的数做移位操作，其阶差为移位量。以下程序选用for循环来完结移位，S(5 downto 0)存储阶差，最大值是32。
然后尾数经加减运算后规格化并输出，为了以规范浮点格局输出，规格化需求前导零检测。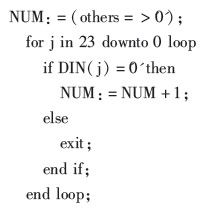
然后进行移位操作，最终将规格化后的数据整合输出，就完结两个浮点数的加法运算。
图6的波形为两个输入浮点数的加法运算数据，以16进制标明。上述数据别离将不同类型的数据分配运算，数据标明该仿真成果正确。
1．3．2 地址发生单元
地址发生单元首要是盯梢FFT运算进展，从而更好地分配存储单元，及操控各相关模块的运转。
(1)经过计数器来盯梢记载FFT核算的状况。为便利对存储单元操作，选用计数器来记载FFT的核算状况。8点的FFT，每个单元包含4个数据，所以用一个4位计数器Butterfly标明悉数的运算状况。一个2位级计数器Stage标明三级蝶形单元。当Butterfly计数为4时，级计数器Stage加1，当Stage计数为3时，标明FFT的核算操作完结。当Butterfly计数为15时，输入输出信号置‘1’，反应回操控器输入输出操作完结。
(2)ROM读取的地址。旋转因子存储在ROM中，由实部cos(2×k×π／8)和虚部sin(2×k×π／8)两部分组成，读取由时钟单元的信号操控。由图2能够看出每一级参与蝶形运算的旋转因子不同。
(3)RAM数据地址。在整个地址单元中，分配RAM中数据的地址是要点，8点蝶形运算共需16个存储单元，数据地址的发生遵从必定规矩。例如，Butterfly的信号为“a3a2a1a0”，则x，y的地址发生规矩如表1所示。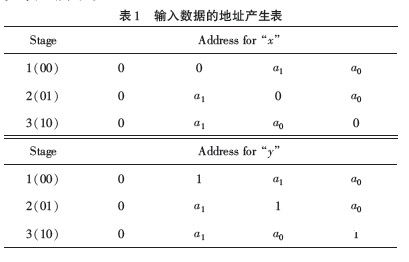
数据的读取靠时钟信号来操控。
1．4 FFT仿真成果剖析
图7中输入8点数据为[-l，1，2，-0．5，-3，-1，2，0]。仿真成果经转化后，用10进制标明的最终成果为[0，3．76775-1．06065i，-8-0．5i，0．23225-1．06065i，0．5，0．23225+1．06065i，-8+0．5i．3．76775+1．06065i]。Matlab仿真后成果为[-0．5000，3．7678-1．0607i，-0．8000-0．5000i，0．2322-1．0607i，0．5000，0．2322+1．0607i，-0．8000+0．5000i，3．7678+1．0607i]两成果很挨近，差错较小，仿真成果正确。
2 结束语
文中在剖析了FFT算法后，描绘了运算的蝶形单元，地址生成单元及FFT的完结进程。从实践规划动身，完结了根据FPGA的单精度浮点运算器的FFT规划，精度到达10-6。其输出成果与Matlab仿真成果附近，到达了使用FPGA完结FFT的意图。
