新的颤动分化图和新的颤动别离办法

跟着信号速率的不断提高和对精度的越来越高要求，需求进行颤动成分的别离以更深化表征颤动特征和查找问题本源。现代（2012年后），大都按下图进行颤动成分的分化。

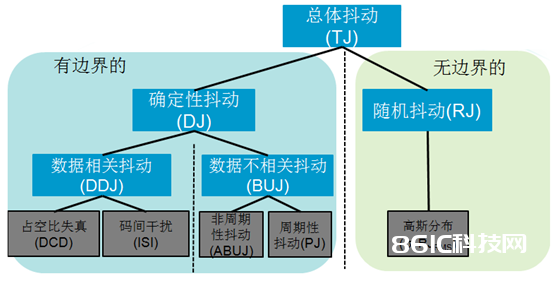
图1 颤动成分分化图

随机颤动RJ

随机颤动是不能猜测的守时噪声，由于它没有可以辨认的形式。典型的随机噪声实例是在无线电接收机调谐到没有活动的载频时听到的声响。虽然在理论上随机进程具有恣意概率散布，但咱们假定随机颤动呈现高斯散布，以树立颤动模型。这种假定的原因之一是，在许多电路中，随机噪声的首要来历是热噪声(也称为 Johnson 噪声或散粒噪声)，而热噪声呈现高斯散布。另一个比较根底的原因是，依据中心极限定理，不论各个噪声源选用什么散布，许多不相关的噪声源的组成效应该挨近高斯散布。高斯散布也称为正态散布，但它的一个最重要的特色是：对高斯变量，它可以到达的峰值是无穷大。虽然这种随机变量的大多数样本将会集合在中心值的周围，但在理论上，任何单一的样本，它可以违背中心值恣意大的量。所以，高斯散布都没有峰到峰鸿沟值，从这种散布中的样本数越多，所测得的峰到峰值将越大。所以，咱们用stdev或RMS(均方差)值来衡量随机颤动RJ。

确定性颤动DJ

确定性颤动是可以重复的、可以猜测的守时颤动。正因如此，这个颤动的峰到峰值具有上下限，在数量相对较少的调查根底上，一般可以以高置信度调查或猜测其鸿沟。DDJ和PJ依据颤动特色和底子成因进一步细分了这类颤动。确定性颤动和随机颤动在计算图上可以用图形象化表明。

RJ和DJ频谱别离法

传统的RJ和DJ的别离办法是频谱别离法，是在频域中取得RJ和PJ，然后在时域中取得DJ，再计算出ISI和DCD。频谱别离法的要害是挑选PJ门限，一般由试验数据得出，经过PJ门限把别离的谱线滤掉，剩下的是RJ频谱，再进行积分即可得到RJrms。

图2频谱别离法进行RJ和PJ别离

假如频谱类似于白噪声，则RJ别离作用较好，可是假如丈量数据缺乏，则或许呈现别的一种状况，如下图所示，则RJ别离就需求细心考虑。这时候在颤动剖析软件中，有两种RJ带宽可供挑选：Wide和Narrow。
什么时候挑选wide或narrow呢？
假如丈量数据量够大，挑选Wide即可。可是假如丈量数据量较小，挑选Narrow更可以确保丈量精度。

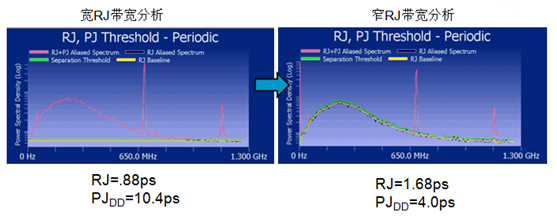
图3 RJ别离带宽的挑选

非周期性颤动ABUJ和高斯尾部拟合别离法

当有串扰呈现时，咱们会发现浴盆曲线中的丈量数据和运用双狄拉克模型仿真的数据接壤不滑润或没有交点的状况，这说明颤动别离是不准确的。所以最近改进了颤动别离的办法，增加了非周期性颤动ABUJ，用于衡量串扰或地弹。

图4 传统的频谱别离法和最新的高斯尾部拟合法在别离有串扰状况下的差异

串扰或地弹导致的波形和计算图的改变如下所示，可见传统的频谱别离丈量办法不能在有串扰或地弹的状况下准确进行颤动别离，而最新选用的高斯尾部拟合规律很好的处理了这个难题。

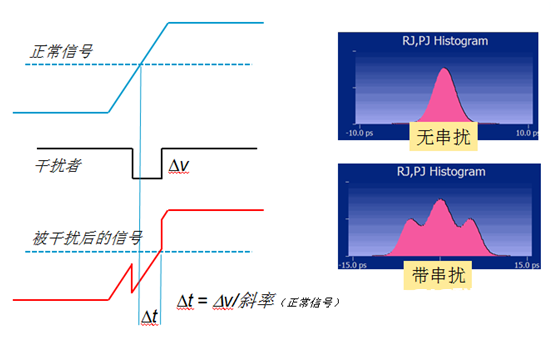
图5 串扰或地弹导致的信号的改变即计算图的改变

高斯尾部拟合颤动别离法都在时域中进行，取得颤动计算图，对左边缘和右边缘散布进行高斯拟合，取得RJ。其实，这个实际操作起来并不简单，恰当挑选拟合窗口是十分要害的。


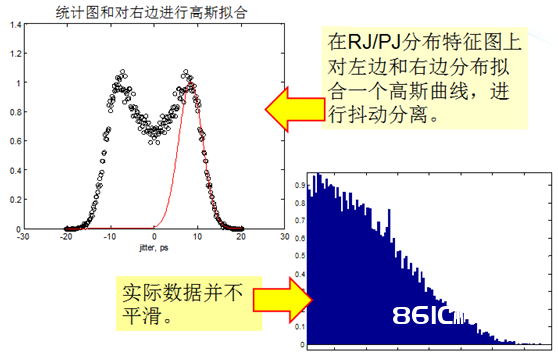
图6 高斯尾部拟合原理

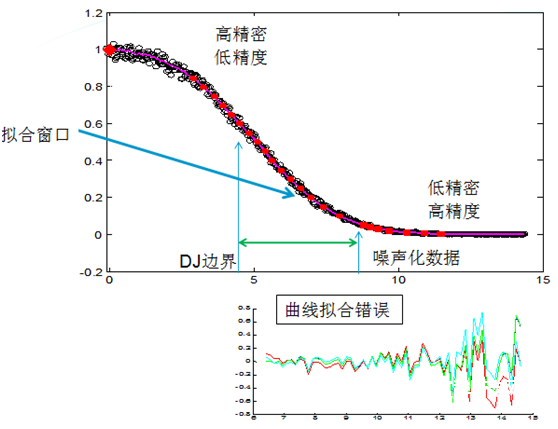
图7 高斯尾部拟合法差错考虑