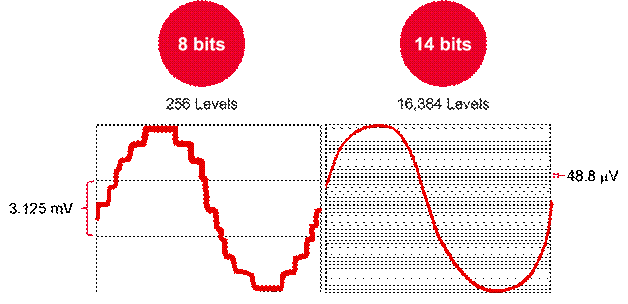
导言
在仿真电路结构时,重要的是能够处理元件的寄生参数或非抱负特性,如非线性品质因数(Q值)、寄生封装电容和引脚电感。这些参数,特别是品质因数,一般能够运用简略的公式在一个有限的频带内近似得到。
像安捷伦的仿真套件ADS或Applied Wave Research公司的Microwave Office等电路仿真器能够对不同的元件值完成与频率有关的变量或公式。因为完成的频率相关公式能够处理元件的非抱负特性,因而能使仿真成果愈加准确和牢靠。
根本模型
电容模型
惯例的电容模型如图1所示。
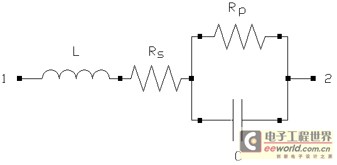
图1:集总元件电容的等效电路模型。
参阅图1,电容的非抱负特性被显现为引线电感(以及电容中的金属层构成的电感)L、因为不完美的金属(有限传导率)引起的引线电阻RS以及因为电介质的不纯引起的传导电阻RP。图1中的串联电阻RS能够由给定的Q值确认,并联电阻RP则由电容内部的介质衰耗因数确认。
图1中的RS一般代表电容的等效串联电阻(ESR),L用于代表器材的谐振频率。同一表贴(SMT)多层电容的谐振频率在不同装置方法下是有改变的,详细取决于水平装置仍是笔直装置。
品质因数Q的频率相关性决议了电容的特性。一般Q因数能够用公式(1)进行简化:
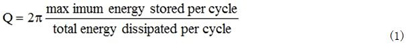
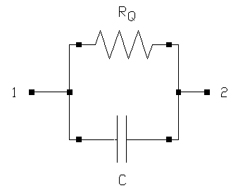
图2:用于确认电容Q值的简化等效电路。电感模型
运用的电感模型愈加简略。图5显现了常用的电感模型,它由抱负电感L和电感电阻R组成。
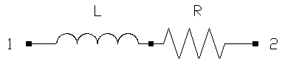
图3:集总元件电感的一般等效模型。
电阻R主要是因为电感器材中的导体阻抗引起的。电感的Q因数取得方法与电容(1)相同,仅有破例是电阻现在选用串联方法建模。

试验和理论成果
将修改后的Q值和电感建模应用于组合式低通滤波器,如图4所示。
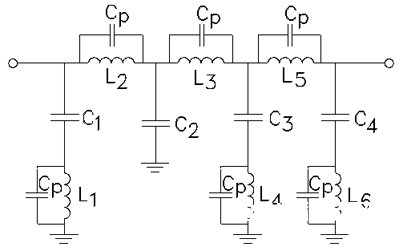
图4:典型集总元件LC低通滤波器的原理图。
这种特别滤波器包括两个切成两份的PI匹配部分(用于将滤波器连接到传输线)、一个稳定k值的T部分(或原型)和一个m派生的T部分。标号为CP的电容是电感的封装寄生参数,被建模为0.12pF数量级的抱负电容。
定论
经过处理%&&&&&%和电感的非抱负特性能够准确猜测滤波器的频率特性。电感的品质因数和电感值不是固定的,或者说在频域上的特性呈线性方法,经过处理频率相关的改变能够得到十分准确的电路建模。
本文中运用的曲线拟合公式矮小简略,能够在比如安捷伦的ADS和Applied Wave Research公司的Microwave Office等电路剖析程序中轻松完成,并能用来处理这些元件中产生的非抱负特性。