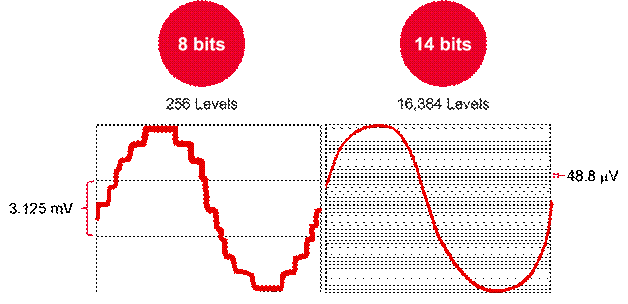
1、限幅滤波法(又称程序判别滤波法)
2、中位值滤波法
3、算术均匀滤波法
4、递推均匀滤波法(又称滑动均匀滤波法)
5、中位值均匀滤波法(又称防脉冲搅扰均匀滤波法)
4、递推均匀滤波法(又称滑动均匀滤波法)
5、中位值均匀滤波法(又称防脉冲搅扰均匀滤波法)
6、限幅均匀滤波法
7、一阶滞后滤波法
8、加权递推均匀滤波法
8、加权递推均匀滤波法
9、消抖滤波法
10、限幅消抖滤波法
11、IIR 数字滤波器
A. 办法:
B. 长处:高通,低通,带通,带阻恣意。规划简略(用matlab)
C. 缺陷:运算量大。
C. 缺陷:运算量大。
//———————————————————————
软件滤波的C程序样例
11种软件滤波办法的示例程序
假定从8位AD中读取数据(假如是更高位的AD可定义数据类型为int),子程序为get_ad();
1、限副滤波
#define A 10
char value;
char filter()
{
}
{
}
2、中位值滤波法
#define N
char filter()
{
}
{
}
3、算术均匀滤波法
#define N 12
char filter()
{
}
{
}
4、递推均匀滤波法(又称滑动均匀滤波法)
#define N 12
char value_buf[N];
char i=0;
char i=0;
char filter()
{
}
{
}
5、中位值均匀滤波法(又称防脉冲搅扰均匀滤波法)
#define N 12
char filter()
{
}
{
}
6、限幅均匀滤波法
略 参阅子程序1、3
略 参阅子程序1、3
7、一阶滞后滤波法
#define a 50
char value;
char filter()
{
}
{
}
8、加权递推均匀滤波法
#define N 12
char code coe[N] = {1,2,3,4,5,6,7,8,9,10,11,12};
char code sum_coe = 1+2+3+4+5+6+7+8+9+10+11+12;
char code sum_coe = 1+2+3+4+5+6+7+8+9+10+11+12;
char filter()
{
}
{
}
9、消抖滤波法
#define N 12
char filter()
{
}
{
}
10、限幅消抖滤波法
略 参阅子程序1、9
11、IIR滤波比如
int
{
}
//——————————————————————————
{
}
//——————————————————————————