ADI:乘法器与调制器

文章转自ADI官网，版权归属原作者一切

尽管许多有关调制的描绘都将其描绘成一种乘法进程，但实践状况更为杂乱。

首要，为明晰起见，若信号Acos)和未调制载波cos(ωt)施加于抱负乘法器的两路输入，则咱们将得到一个调制器。这是因为两个周期波形A_scos(ω_st) 和 A_ccos(ω_ct)施加于乘法器（为便于剖析，假定份额因子为1 V）输入端，发作的输出为：

    V_o(t) = ½A_sA_c[cos((ω_s + ω_c)t) + cos(ω_s – ω_c)t))]

若载波A_ccos(ω_ct)起伏为1 V (A_c = 1)，则该式进一步简化为：

    V_o(t) = ½A_s[cos((ω_s + ω_c)t) + cos((ω_s – ω_c)t)]

但在大多数状况下，调制器是履行此功用更好的电路。调制器（用来改动频率的时分也称为混频器）与乘法器密切相关。乘法器的输出是其输入的瞬时积。调制器的输出是该调制器其间一路输入的信号（称为信号输入）和另一路输入的信号符号（称为载波输入）的瞬时积。图1所示为调制函数的两种建模办法：作为放大器运用，经过载波输入上的比较器输出切换正增益和负增益；或许作为乘法器运用，并在其载波输入和其间一个端口之间放置一个高增益限幅放大器。两种架构都可用来构成调制器，但开关放大器架构（用于AD630平衡调制器中）运转较慢。大多数高速IC调制器含有一个跨导线性乘法器（根据吉尔伯特单元），并在载波途径上有一个限幅放大器，用来过驱其间一路输入。该限幅放大器或许具有高增益，答应低电平载波输入——或许具有低增益和洁净的限幅特性，然后要求相对较大的载波输入以正常作业。详细信息请参阅数据手册。

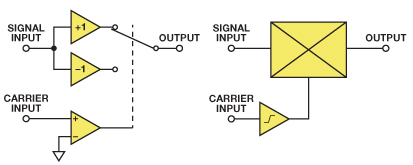
出于某些原因，咱们运用调制器而非乘法器。乘法器的两个端口均为线性，因而载波输入的任何噪声或调制信号都会与信号输入相乘，下降输出；一起，大多数状况下可疏忽调制器载波输入的起伏变化。二阶特性会导致载波输入的起伏噪声影响输出，但最好的调制器都会尽或许削减这种影响，因而不归入本文的评论规模。简略的调制器模型运用由载波驱动的开关。（抱负）开路开关具有无限大的电阻和零热噪声电流，且（抱负）闭路开关具有零电阻和零热噪声电压；因而，尽管调制器的开关并非抱负，但比较乘法器而言，调制器仍然具有较低的内部噪声。别的，比起乘法器，规划与制作相似的高性能、高频率调制器也更为简洁。

与模拟乘法器相同，调制器将两路信号相乘；但与模拟乘法器不同的是，调制器的乘法运算对错线性的。当载波输入的极性为正时，信号输入乘以+1；而当极性为负时，则乘以–1。换言之，信号乘以载波频率下的方波。

频率为ω_ct 的方波可运用傅里叶序列的奇次谐波表明：

    K[cos(ω_ct) – 1/3cos(3ω_ct) + 1/5cos(5ω_ct) – 1/7cos(7ω_ct) + …]

对该序列求和：[+1, –1/3, +1/5, –1/7 + …] 为 π/4。因而，K数值为4/π，这样当正直流信号施加到载波输入时，平衡调制器可作为单位增益放大器运用。

载波起伏并不重要，只需它足够大，可驱动限幅放大器即可；因而，由信号A_scos(ω_st)和载波 cos(ω_ct)驱动的调制器发作的输出即为信号与载波平方的乘积：

    2As/π[cos(ω_s + ω_c)t + cos(ω_s – ω_c)t –

        1/3{cos(ω_s + 3ω_c)t + cos(ω_s – 3ω_c)t} +

        1/5{cos(ω_s + 5ω_c)t + cos(ω_s – 5ω_c)t} –

        1/7{cos(ω_s + 7ω_c)t + cos(ω_s – 7ω_c)t} + …]

该输出包括下列项的频率之和与频率之差：信号与载波、信号与载波的一切奇次谐波。抱负的完美平衡调制器中不存在偶次谐波乘积。但是在实在调制器中，载波端口的剩余失调会导致低电平偶次谐波乘积。在许多运用中，低通滤波器(LPF)可滤除高次谐波乘积项。请记住，cos(A) = cos(–A), 因而 cos(ω_m – Nω_c)t = cos(Nω_c – ω_m)t，而且无需忧虑“负”频率。滤波处理后，调制器输出可计算如下：

    2As/π[cos(ω_s + ω_c)t + cos(ω_s – ω_c)t]

它和乘法器输出的表达式共同，仅仅增益稍有不同。在实践体系中，增益选用放大器或衰减器进行归一化，因而此处无需考虑不同体系的理论增益。

在简略的运用中，明显运用调制器优于运用乘法器，但怎么界说“简略”？调制器用作混频器时，信号和载波输入分别为频率等于f₁ 和 f_c的简略正弦波，未经滤波处理的输出包括频率和 (f₁ + f_c) 与频率差 (f₁ – f_c) ，以及信号与载波奇次谐波的频率和与频率差 (f₁ + 3f_c), (f₁ – 3f_c), (f₁ + 5f_c), (f₁ – 5f_c), (f₁ + 7f_c), (f₁ – 7f_c)。经LPF滤波之后，估计仅得到基波项 (f₁ +f_c) 和 (f₁ –f_c)。

但是，若 (f₁ + f_c) > (f₁ – 3f_c)，将无法运用简略的LPF区别基波与谐波项，因为某个谐波项的频率低于某个基波项。这并非归于简略的状况，因而需进一步剖析。

假如假定信号包括单一频率f₁，或假定信号更杂乱，散布在频段f₁至 f₂中，则咱们便可剖析调制器的输出频谱，如下图所示。假定完美平衡的调制器不存在信号走漏、载波走漏或失真，则输出不含输入项、载波项和杂散项。输入以黑色表明（或在输出图中以浅灰色表明，哪怕实践上并不存在）。

图2显现输入—坐落 f₁ 至 f₂ 频段内的信号，以及频率为 f_c的载波。乘法器不含下列奇次载波谐波：1/3(3f_c), 1/5(5f_c), 1/7(7f_c)…，以虚线表明。请注意，小数1/3、1/5和1/7表明起伏，而非频率。

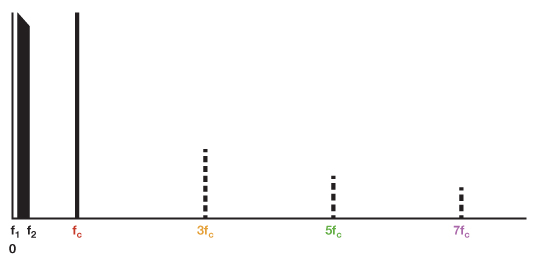
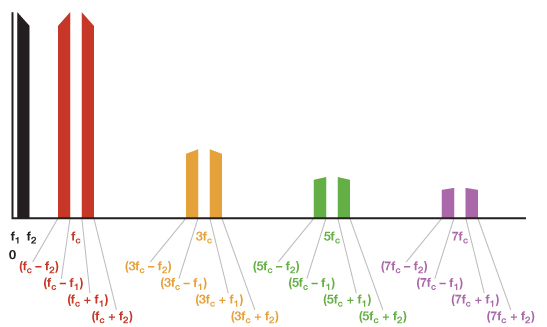
图3显现乘法器或调制器的输出，以及截止频率为2fc的LPF。

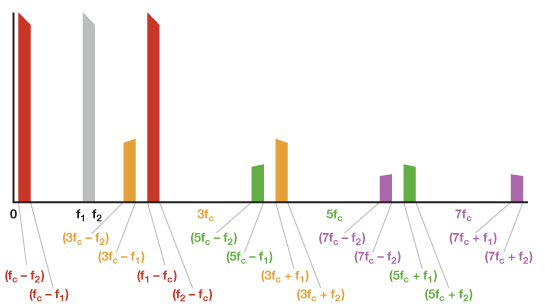
图4显现未经滤波处理的调制器输出（但不含7f_c以上的谐波项）。

若信号频带f₁ 至 f₂坐落奈奎斯特频带（直流至 f_c/2）内，则截止频率高于2f_c的LPF将使调制器具有与乘法器相同的输出频谱。若信号频率高于奈奎斯特频率，则状况更杂乱。

图5显现信号频带正好低于f_c时将发作的状况。仍然有或许别离谐波项和基波项，但此刻需运用具有峻峭滚降特性的LPF。

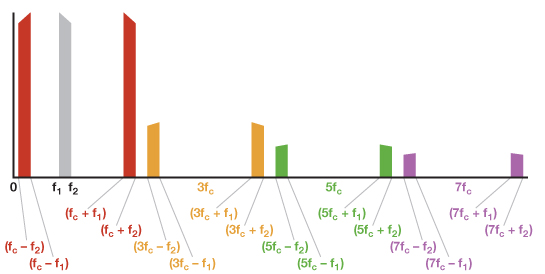
图6显现因为f_c坐落信号通带内，谐波项叠加 (3f_c – f₁) < (f_c + f₁)，因而，基波项不再可以经过LPF与谐波项别离。所需信号此刻有必要经过带通滤波器(BPF)进行挑选。

所以，尽管调制器在大部分变频运用中优于线性乘法器，但规划实践体系时有必要考虑到它们的谐波项。

参阅电路

Analog Dialogue 

Brandon, David. “Multichannel DDS Enables Phase-Coherent FSK Modulation.” Analog Dialogue, Volume 44, Number 4, 2010.

Gilbert, Barrie. “Considering Multipliers (Part 1).” Analog Dialogue, Volume 42, Number 4, 2008.

Product Pages 

Mixers/Multipliers

Multipliers/Dividers

Modulators/Demodulators

RAQs 

Multipliers and Modulators 

Caveat Emptor

Tutorials 

MT-079: Analog Multipliers 

MT-080: Mixers and Modulators