NTC热敏电阻是一种电阻式传感器，具有电阻温度系数大、型小体轻、热惯性小、安稳牢靠、价格便宜、结构简略等特色，使它广泛使用于家庭空调、汽车空调、冷柜、冰箱等需求温度丈量和操控的场合。但NTC热敏电阻对错线性元件，且自身具有自热效应，需求规划测温体系战胜这两方面的缺点。常用于处理NTC热敏电阻非线性的办法有经历公式法、最小二乘拟合法、硬件电路补偿法和恒源法结合软件查表法.经历公式法核算较为杂乱，在较宽温度规模内精度不够高。最小二乘法需求在得到很多的试验数据下进行，工作量较大，占用内存也较大。硬件电路补偿法对电子元器件的要求较高，跟着电路的杂乱度的添加，一同也带来了电路附加差错。恒源法结合软件查表法需求占用较大存储空间。针对以上办法的缺乏，提出了一种三阶对数公式分段曲线拟合法，因为用于船用柴油机，不只要丈量温度，还有机油压力等需求丈量，因而选用的是压力温度合二为一的传感器小论文，丈量温度运用的是NTC热敏电阻，硬件部分对NTC热敏电阻共地和不共地以及分档测验进行了讨论，软件部分对NTC热敏电阻进行对数分段曲线拟合以及选用滑动滤波的算法减小A/D采样引起的差错。
1 R-T三阶对数公式的推导
NTC热敏电阻根本的R-T特性可用指数函数式表明：
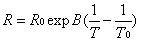（1）
式中R为绝对温度为T时的零功率电阻值（
）。零功率电阻值指在规则的温度时，选用引起电阻值改变相关于总的丈量差错来说能够忽略不计的值［3］；R0 为绝对温度为T0时的零功率电阻值（）。B为与热敏电阻资料、结构有关的敏感度系数，是以零功率电阻对时间的改变巨细来表明的，它是由电阻-温度特性就任两点温度，求出的系数，不同的两点求出的B值是不同的，因而不能依据厂家给出的B值参阅规模去丈量温度，会带来较大的差错。
图1为本文选用的NTC热敏电阻在0℃~120℃之间电阻R与摄氏温度T的联系曲线。
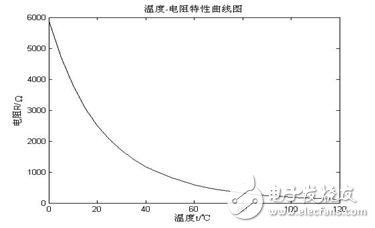
图1 NTC热敏电阻电阻-温度特性图
由图1能够看出NTC热敏电阻值与温度之间存在着严峻的非线性，一般关于非线性的曲线拟合处理都是在公式（1）的基础上进行的，可对公式（1）进行对数改换，使得温度T和电阻R的自然对数近似呈线性联系小论文，并在此基础上进行多项式打开和分段曲线拟合。
对等式（1）两头一同取自然对数，进行运算后可得下式：
但文中一切的数据核算均选用微处理器完成，触及自然对数和平方、三次方等的运算，归纳考虑精度和实时性的要求，去掉平方项，得式（7）。经试验验证，能到达精度要求，又提高了程序的运转速度。由图1可看出NTC热敏电阻在40℃、80℃处的温度-电阻改变较大，若在整个区间规模内都选用同一个多项式进行拟合，则差错较大。选用对数分段曲线拟合，又考虑到微处理器处理数据时各区间并不是彼此无关小论文，而是彼此有堆叠，所以分红［0℃，40℃］，［30℃，80℃］，［70℃，120℃］3个区间。
y= H0+ H1x + H3x3（7）
因而需求在这3个区间内求解3组不同的系数H0、H1、H3。依据热敏电阻厂家供给的温度-电阻值表，选取其间的3个点，可选用一般多项式法、最小二乘法和切比雪夫多项式法［6］对三个系数进行核算，但在本文中该三种办法的准确度相差不大。 因而选用算法最简略的一般多项式法进行核算，可得以下三个拟合方程：
由此，实践使用可依据以上三个方程进行软硬件的规划。
2 NTC热敏电阻分段曲线拟合的硬件丈量电路
选用的NTC热敏电阻将丈量水温文油温的NTC热敏电阻组装在了一同，丈量油温的NTC热敏电阻自身有一端是接地的，丈量水温的NTC热敏电阻两头均不接地。因而硬件丈量电路中有必要考虑NTC热敏电阻的共地与不共地问题。NTC热敏电阻跟着温度的升高而阻值变小，0℃时阻值为5895，120℃时阻值为112.7。考虑到热敏电阻的自热效应小论文，流过NTC热敏电阻的电流不得超越1
，选定为0.5，选用恒流源为热敏电阻供给0.5的电流。在0℃时NTC热敏电阻两头的电压大约为3V，在120℃时NTC热敏电阻两头的电压约为0.05V，0.05V的信号太小，单片机的A/D口进行采样后得到的信号十分弱，有必要对NTC热敏电阻信号进行分档倍乘后收集，硬件丈量电路框图如图2所示。
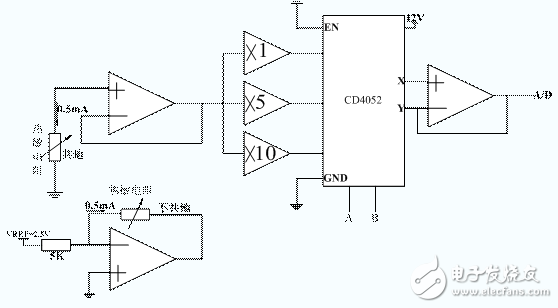
图2 热敏电阻硬件丈量电路
由图1可知热敏电阻共地和不共地的电路接法。分为1倍、5倍、10倍三档，1倍档对应于［0℃，40℃］温度区间，它对应的A/D口电压规模为0.5V~3V，若A/D口电压低于0.5V小论文，则选用5倍档进行丈量；5倍档对应于［30℃，80℃］温度区间，它对应的A/D口电压规模为0.1V~0.9V，若A/D口电压低于0.1V，则选用10倍档进行丈量；10倍档对应于［70℃，120℃］温度区间。选用4通道数字操控模仿开关CD4052对倍乘档进行挑选。该热敏电阻用于丈量船用柴油机的水温文油温，水油温高于97℃时进行报警。
3 NTC热敏电阻分段曲线拟合的软件规划
3.1 A/D采样的滑动滤波算法
A/D口在对温度数据进行收集时会发生差错，选用滑动滤波算法减小该差错。如图3所示为滑动滤波算法框图。
图3 滑动滤波算法框图
如图3所示，将收集的温度数据放到一个行列中，在刚开始进行收集温度数据时，为避免搅扰，接连收集16次后再对此16个数据求和并求均匀，行将和右移4位。尔后小论文，取8位求和并取均匀，行将和右移3位，采样一次做一次均匀，均匀后的数据准确度更高。
3.2 R-T转化的程序完成
硬件电路把电阻的改变转化为了电压的改变，并对电压进行分档收集。要丈量出温度值，需求依托程序来完成。如图4所示为水温的R-T转化的程序流程图，油温的R-T转化相似，将不再叙说。对收集的温度数据即已转化为电压的数据进行判别，假如电压在［0.5V，3V］规模
内，则电压处于1倍档，温度值处于［0℃，40℃］温度区间内小论文，因而选用公式（8）进行核算；假如电压在［0.1V，0.9V］规模内，则电压处于5倍档，温度值处于［30℃，80℃］温度区间内，因而选用公式（9）进行核算。假如电压不处于以上两个区间，则直接选用10倍档的温度公式（10）进行核算，不必再进行判别。
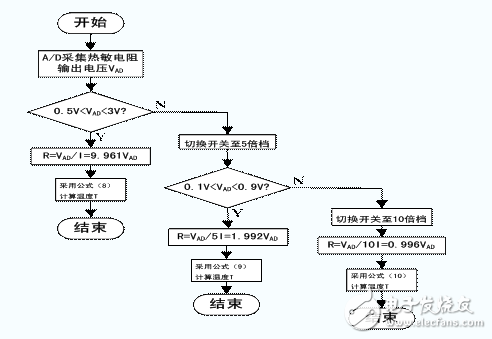
图4 水温R-T转化程序流程图
4 试验成果及剖析
依据三个曲线拟合方程，并进行软硬件规划组成的测温体系进行试验测验得到的拟合数据和差错如表1所示：
表1 试验丈量拟合温度/拟合差错
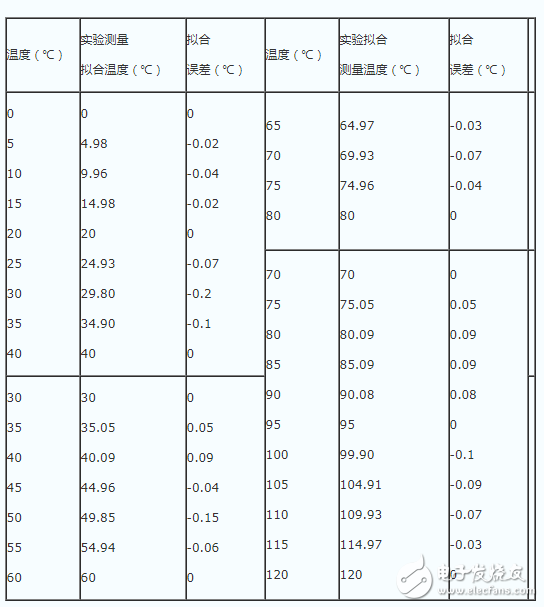
由表1能够发现，选用对数分段曲线拟合的拟合差错在30℃时最大约为0.2℃，原因可能是因为非线性改换形成的，但总的来说，拟合精度仍是不错的。体系硬件选用了毫安级恒流源降低了热敏电阻的自热效应小论文，软件选用了滑动滤波的算法削减A/D转化带来的差错，体系软硬件结合完成了对数分段曲线拟合，为整个测温体系供给了精度较高、实时性较好的丈量。
5 结束语
NTC热敏电阻选用对数分段曲线拟合的方法，对NTC热敏电阻的电阻-温度特性公式进行了改换，在近似呈线性的条件下对温度进行分段曲线拟合，精度较高。去掉平方项，提高了微处理器的运算速度。编程较易完成，程序运算速度较快，实时性较好。只需更改拟合多项式的系数即可对其他类型的NTC热敏电阻进行拟合，互换性强。在0℃~120℃温度规模，对数分段曲线拟合的拟合精度要优于一般多项式拟合。该计划在理论的验证下，已经过编程完成，经过厂家的检验，已交给厂家使用到船用柴油机进行实践测温，运转正常。
