前语
最近计划体系学习下机器学习的根底算法,防止眼高手低,决议把常用的机器学习根底算法都完成一遍以便加深形象。本文为这系列博客的第一篇,关于决议计划树(Decision Tree)的算法完成,文中我将对决议计划树种触及到的算法进行总结并附上自己相关的完成代码。一切算法代码以及用于相应模型的练习的数据都会放到GitHub上(https://github.com/PytLab/MLBox).
本文中我将一步步经过MLiA的隐形眼镜处方数集构建决议计划树并运用Graphviz将决议计划树可视化。
正文
决议计划树学习
决议计划树学习是依据数据的特点选用树状结构树立的一种决议计划模型,能够用此模型处理分类和回归问题。常见的算法包含 CART(Classification And Regression Tree), ID3, C4.5等。咱们往往依据数据集来构建一棵决议计划树,他的一个重要任务便是为了数据中所包含的常识信息,并提取出一系列的规矩,这些规矩也便是树结构的创立进程便是机器学习的进程。
决议计划树的结构
以下面一个简略的用所以否买电脑猜测的决议计划树为比如,树中的内部节点表明某个特点,节点引出的分支表明此特点的一切或许的值,叶子节点表明终究的判别成果也便是类型。
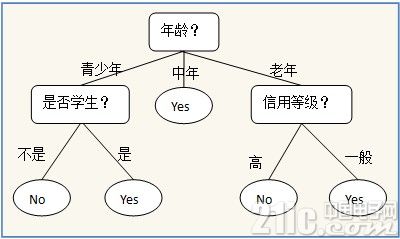
凭借可视化东西例如Graphviz,matplotlib的注解等等都能够讲咱们创立的决议计划树模型可视化并直接被人了解,这是贝叶斯神经网络等算法没有的特性。
决议计划树算法
决议计划树算法首要是指决议计划树进行创立中进行树割裂(区分数据集)的时分选取最优特征的算法,他的首要意图便是要选取一个特征能够将分隔的数据集尽量的规整,也便是尽或许的纯. 最大的准则便是: 将无序的数据变得愈加有序。
这儿总结下三个常用的办法:
1.信息增益(information gain)
2.增益比率(gain ratio)
3.基尼不纯度(Gini impurity)
信息增益 (Information gain)
这儿触及到了信息论中的一些概念:某个事情的信息量,信息熵,信息增益等, 关于事情信息的浅显解说能够看知乎上的一个答复
某个事情 i 的信息量: 这个事情产生的概率的负对数
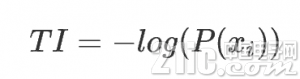
信息熵便是均匀而言一个事情产生得到的信息量巨细,也便是信息量的期望值
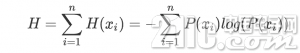
任何一个序列都能够获取这个序列的信息熵,也便是将此序列分类后核算每个类型的概率,再用上述公式核算,运用Python完成如下:
def get_shanno_entropy(self, values):
”’ 依据给定列表中的值核算其Shanno Entropy
”’
uniq_vals = set(values)
val_nums = {key: values.count(key) for key in uniq_vals}
probs = [v/len(values) for k, v in val_nums.items()]
entropy = sum([-prob*log2(prob) for prob in probs])
return entropy
信息增益
咱们将一组数据集进行区分后,数据的信息熵会产生改动,咱们能够经过运用信息熵的核算公式别离核算被区分的子数据集的信息熵并核算他们的均匀值(期望值)来作为切割后的数据集的信息熵。新的信息熵的比较未区分数据的信息熵的减小值便是信息增益了. 这儿我在开始就了解错了,所以写出的代码并不能创立正确的决议计划树。
假定咱们将数据集D区分红kk 份D1,D2,…,Dk,则区分后的信息熵为:
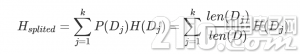
信息增益便是两个信息熵的差值
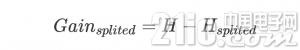
在这儿我首要运用信息增益来进行特点挑选,详细的完成代码如下:
def choose_best_split_feature(self, dataset, classes):
”’ 依据信息增益确认最好的区分数据的特征
:param dataset: 待区分的数据集
:param classes: 数据集对应的类型
:return: 区分数据的增益最大的特点索引
”’
base_entropy = self.get_shanno_entropy(classes)
feat_num = len(dataset[0])
entropy_gains = []
for i in range(feat_num):
splited_dict = self.split_dataset(dataset, classes, i)
new_entropy = sum([
len(sub_classes)/len(classes)*self.get_shanno_entropy(sub_classes)
for _, (_, sub_classes) in splited_dict.items()
])
entropy_gains.append(base_entropy – new_entropy)
return entropy_gains.index(max(entropy_gains))
增益比率
增益比率是信息增益办法的一种扩展,是为了战胜信息增益带来的弱泛化的缺点。由于依照信息增益挑选,总是会倾向于挑选分支多的特点,这样会是的每个子集的信息熵最小。例如给每个数据增加一个第一无二的id值特征,则依照这个id值进行分类是取得信息增益最大的,这样每个子会集的信息熵都为0,可是这样的分类便没有任何含义,没有任何泛化才能,相似过拟合。
因而咱们能够经过引进一个割裂信息来找到一个更适宜的衡量数据区分的规范,即增益比率。
割裂信息的公式表明为:
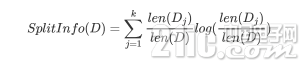
可见假如数据分的越多,割裂信息的值就会越大
这时分把割裂信息的值放到分母上便会中和信息增益带来的坏处。
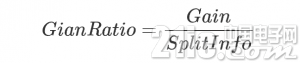
当然SplitInfo有或许趋近于0,这个时分增益比率就会变得非常大而不可信,因而有时还需在分母上增加一个滑润函数,详细的能够参阅参阅部分列出的文章
基尼不纯度(Gini impurity)
基尼不纯度的界说:

其间m 表明数据集D 中类别的个数, pi 表明某种类型呈现的概率。可见当只要一种类型的时分基尼不纯度的值为0,此刻不纯度最低。
针对区分红k个子数据集的数据集的基尼不纯度能够经过如下式子核算:
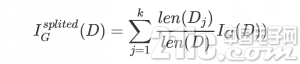
由此咱们能够依据不纯度的改变来选取最有的树割裂特点

树割裂
有了选取最佳割裂特点的算法,下面咱们就需求依据挑选的特点来将树进一步的割裂。所谓树割裂只不过是依据挑选的特点将数据集区分,然后在总区分出来的数据会集再次调用选取特点的办法选取子数据集的中特点。完成的最好方法便是递归了.
关于用什么数据结构来表明决议计划树,在Python中能够运用字典很便利的表明决议计划树的嵌套,一个树的根节点便是特点,特点对应的值又是一个新的字典,其间key为特点的或许值,value为新的子树。
下面是我运用Python完成的依据数据集创立决议计划树:
def create_tree(self, dataset, classes, feat_names):
”’ 依据当时数据集递归创立决议计划树
:param dataset: 数据集
:param feat_names: 数据会集数据相应的特征称号
:param classes: 数据会集数据相应的类型
:param tree: 以字典方式回来决议计划树
”’
# 假如数据会集只要一种类型中止树割裂
if len(set(classes)) == 1:
return classes[0]
# 假如遍历完一切特征,回来份额最多的类型
if len(feat_names) == 0:
return get_majority(classes)
# 割裂创立新的子树
tree = {}
best_feat_idx = self.choose_best_split_feature(dataset, classes)
feature = feat_names[best_feat_idx]
tree[feature] = {}
# 创立用于递归创立子树的子数据集
sub_feat_names = feat_names[:]
sub_feat_names.pop(best_feat_idx)
splited_dict = self.split_dataset(dataset, classes, best_feat_idx)
for feat_val, (sub_dataset, sub_classes) in splited_dict.items():
tree[feature][feat_val] = self.create_tree(sub_dataset,
sub_classes,
sub_feat_names)
self.tree = tree
self.feat_names = feat_names
return tree
树割裂的停止条件有两个
一个是遍历完一切的特点
能够看到,在进行树割裂的时分,咱们的数据会集的数据向量的长度是不断缩短的,当缩短到0时,阐明数据集现已将一切的特点竭尽,便也割裂不下去了, 这时咱们选取终究子数据会集的众数作为终究的分类成果放到叶子节点上.
另一个是新区分的数据会集只要一个类型。
若某个节点所指向的数据集都是同一种类型,那天然没有必要在割裂下去了即便特点还没有遍历完.
构建一棵决议计划树
这我用了一下MLiA书上顺便的隐形眼镜的数据来生成一棵决议计划树,数据中包含了患者眼部情况以及医师引荐的隐形眼镜类型.
首要先导入数据并将数据特征同类型分隔作为练习数据用于生成决议计划树
from trees import DecisionTreeClassifier
lense_labels = [‘age’, ‘prescript’, ‘astigmatic’, ‘tearRate’]
X = []
Y = []
with open(‘lenses.txt’, ‘r’) as f:
for line in f:
comps = line.strip().split(‘t’)
X.append(comps[: -1])
Y.append(comps[-1])
生成决议计划树:
clf = DecisionTreeClassifier()
clf.create_tree(X, Y, lense_labels)
检查生成的决议计划树:
In [2]: clf.tree
Out[2]:
{‘tearRate’: {‘normal’: {‘astigmatic’: {‘no’: {‘age’: {‘pre’: ‘soft’,
‘presbyopic’: {‘prescript’: {‘hyper’: ‘soft’, ‘myope’: ‘no lenses’}},
‘young’: ‘soft’}},
‘yes’: {‘prescript’: {‘hyper’: {‘age’: {‘pre’: ‘no lenses’,
‘presbyopic’: ‘no lenses’,
‘young’: ‘hard’}},
‘myope’: ‘hard’}}}},
‘reduced’: ‘no lenses’}}
可视化决议计划树
直接经过嵌套字典表明决议计划树对人来说欠好了解,咱们需求凭借可视化东西可视化树结构,这儿我将运用Graphviz来可视化树结构。为此完成了讲字典表明的树生成Graphviz Dot文件内容的函数,大致思维便是递归获取整棵树的一切节点和衔接节点的边然后将这些节点和边生成Dot格局的字符串写入文件中并绘图。
递归获取树的节点和边,其间运用了uuid给每个节点增加了id特点以便将相同特点的节点区分隔.
def get_nodes_edges(self, tree=None, root_node=None):
”’ 回来树中一切节点和边
”’
Node = namedtuple(‘Node’, [‘id’, ‘label’])
Edge = namedtuple(‘Edge’, [‘start’, ‘end’, ‘label’])
if tree is None:
tree = self.tree
if type(tree) is not dict:
return [], []
nodes, edges = [], []
if root_node is None:
label = list(tree.keys())[0]
root_node = Node._make([uuid.uuid4(), label])
nodes.append(root_node)
for edge_label, sub_tree in tree[root_node.label].items():
node_label = list(sub_tree.keys())[0] if type(sub_tree) is dict else sub_tree
sub_node = Node._make([uuid.uuid4(), node_label])
nodes.append(sub_node)
edge = Edge._make([root_node, sub_node, edge_label])
edges.append(edge)
sub_nodes, sub_edges = self.get_nodes_edges(sub_tree, root_node=sub_node)
nodes.extend(sub_nodes)
edges.extend(sub_edges)
return nodes, edges
生成dot文件内容
def dotify(self, tree=None):
”’ 获取树的Graphviz Dot文件的内容
”’
if tree is None:
tree = self.tree
content = ‘digraph decision_tree {n’
nodes, edges = self.get_nodes_edges(tree)
for node in nodes:
content += ‘ {} [label={}];n’.format(node.id, node.label)
for edge in edges:
start, label, end = edge.start, edge.label, edge.end
content += ‘ {} -> {} [label={}];n’.format(start.id, end.id, label)
content += ‘}’
return content
隐形眼镜数据生成Dot文件内容如下:
digraph decision_tree {
959b4c0c-1821-446d-94a1-c619c2decfcd [label=call];
18665160-b058-437f-9b2e-05df2eb55661 [label=to];
2eb9860d-d241-45ca-85e6-cbd80fe2ebf7 [label=your];
bcbcc17c-9e2a-4bd4-a039-6e51fde5f8fd [label=areyouunique];
ca091fc7-8a4e-4970-9ec3-485a4628ad29 [label=02073162414];
aac20872-1aac-499d-b2b5-caf0ef56eff3 [label=ham];
18aa8685-a6e8-4d76-bad5-ccea922bb14d [label=spam];
3f7f30b1-4dbb-4459-9f25-358ad3c6d50b [label=spam];
44d1f972-cd97-4636-b6e6-a389bf560656 [label=spam];
7f3c8562-69b5-47a9-8ee4-898bd4b6b506 [label=i];
a6f22325-8841-4a81-bc04-4e7485117aa1 [label=spam];
c181fe42-fd3c-48db-968a-502f8dd462a4 [label=ldn];
51b9477a-0326-4774-8622-24d1d869a283 [label=ham];
16f6aecd-c675-4291-867c-6c64d27eb3fc [label=spam];
adb05303-813a-4fe0-bf98-c319eb70be48 [label=spam];
959b4c0c-1821-446d-94a1-c619c2decfcd -> 18665160-b058-437f-9b2e-05df2eb55661 [label=0];
18665160-b058-437f-9b2e-05df2eb55661 -> 2eb9860d-d241-45ca-85e6-cbd80fe2ebf7 [label=0];
2eb9860d-d241-45ca-85e6-cbd80fe2ebf7 -> bcbcc17c-9e2a-4bd4-a039-6e51fde5f8fd [label=0];
bcbcc17c-9e2a-4bd4-a039-6e51fde5f8fd -> ca091fc7-8a4e-4970-9ec3-485a4628ad29 [label=0];
ca091fc7-8a4e-4970-9ec3-485a4628ad29 -> aac20872-1aac-499d-b2b5-caf0ef56eff3 [label=0];
ca091fc7-8a4e-4970-9ec3-485a4628ad29 -> 18aa8685-a6e8-4d76-bad5-ccea922bb14d [label=1];
bcbcc17c-9e2a-4bd4-a039-6e51fde5f8fd -> 3f7f30b1-4dbb-4459-9f25-358ad3c6d50b [label=1];
2eb9860d-d241-45ca-85e6-cbd80fe2ebf7 -> 44d1f972-cd97-4636-b6e6-a389bf560656 [label=1];
18665160-b058-437f-9b2e-05df2eb55661 -> 7f3c8562-69b5-47a9-8ee4-898bd4b6b506 [label=1];
7f3c8562-69b5-47a9-8ee4-898bd4b6b506 -> a6f22325-8841-4a81-bc04-4e7485117aa1 [label=0];
7f3c8562-69b5-47a9-8ee4-898bd4b6b506 -> c181fe42-fd3c-48db-968a-502f8dd462a4 [label=1];
c181fe42-fd3c-48db-968a-502f8dd462a4 -> 51b9477a-0326-4774-8622-24d1d869a283 [label=0];
c181fe42-fd3c-48db-968a-502f8dd462a4 -> 16f6aecd-c675-4291-867c-6c64d27eb3fc [label=1];
959b4c0c-1821-446d-94a1-c619c2decfcd -> adb05303-813a-4fe0-bf98-c319eb70be48 [label=1];
}
这样咱们便能够运用Graphviz将决议计划树制作出来
with open(‘lenses.dot’, ‘w’) as f:
dot = clf.tree.dotify()
f.write(dot)
dot -Tgif lenses.dot -o lenses.gif
作用如下:
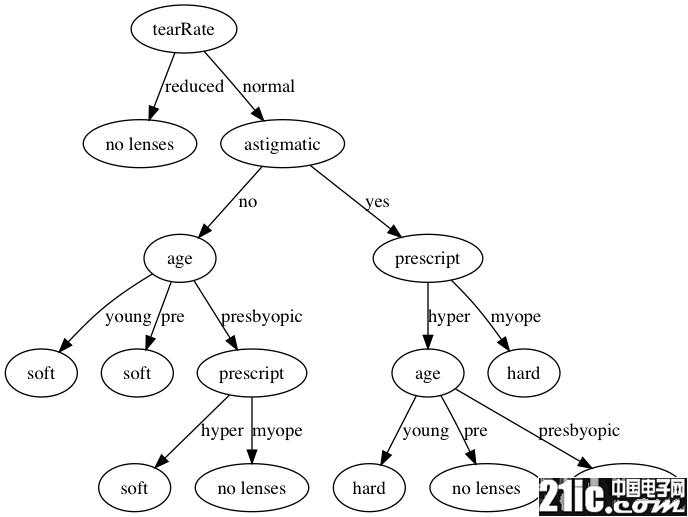
运用生成的决议计划树进行分类
对不知道数据进行猜测,首要是依据树中的节点递归的找到叶子节点即可。z这儿能够经过为递归进行优化,代码完成如下:
def classify(self, data_vect, feat_names=None, tree=None):
”’ 依据构建的决议计划树对数据进行分类
”’
if tree is None:
tree = self.tree
if feat_names is None:
feat_names = self.feat_names
# Recursive base case.
if type(tree) is not dict:
return tree
feature = list(tree.keys())[0]
value = data_vect[feat_names.index(feature)]
sub_tree = tree[feature][value]
return self.classify(feat_names, data_vect, sub_tree)
决议计划树的存储
经过字典表明决议计划树,这样咱们能够经过内置的pickle或许json模块将其存储到硬盘上,一起也能够从硬盘中读取树结构,这样在数据集很大的时分能够节约构建决议计划树的时刻.
def dump_tree(self, filename, tree=None):
”’ 存储决议计划树
”’
if tree is None:
tree = self.tree
with open(filename, ‘w’) as f:
pickle.dump(tree, f)
def load_tree(self, filename):
”’ 加载树结构
”’
with open(filename, ‘r’) as f:
tree = pickle.load(f)
self.tree = tree
return tree
总结
本文一步步完成了决议计划树的完成, 其间运用了ID3算法确认最佳区分特点,并经过Graphviz可视化了构建的决议计划树。