一、集成门电路
数字集成电路按其内部有源器材的不同能够分为两大类：一类为双极型晶体管集成电路（TTL电路）；另一类为单极型集成电路（MOS管组成的电路）。
1．TTL集成逻辑门电路
（1）TTL与非门
CT74S肖特基系列TTL与非门的电路组成如图2-19（a）所示，它由输入级、中间级、输出级3个部分组成。
图2-19 TTL与非门电路图
输入级：由多发射极管VT1和电阻R1组成，多发射极管的3个发射结为3个PN结。其作用是对输入变量A、B、C完结逻辑与，所以它相当于一个与门。
中间级：由VT2、R2和VT6、RB、RC组成，VT2集电极和发射极一起输出两个逻辑电平相反的信号，用以驱动VT3和VT5。
输出级：由VT3、VT4、VT5和R4、R5组成，它采用了达林顿结构，VT3和VT4组成复合管降低了输出高电平时的输出电阻，提高了带负载才能。
TTL 与非门的逻辑符号如图 2-19（b）所示；逻辑表达式为：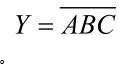
对图2-19所示电路，假如高电平用1表明，低电平用0表明，则可列出图2-19所示的真值表，如表2-1所示。
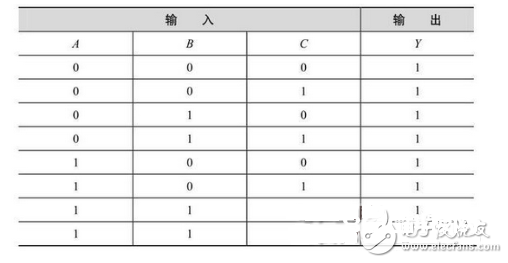
表2-1 TTL与非门真值表
（2）集电极开路与非门（OC门）
① 作业原理。
集电极开路与非门也叫 OC 门，能使门电路输出的电压高于电路的高电平电压值，且门电路的输出端能够并联以完结逻辑与功用，即线与（一般的TTL门电路不能线与）。
OC门的电路如图2-20（a）所示，逻辑符号如图2-20（b）所示，逻辑表达式为：
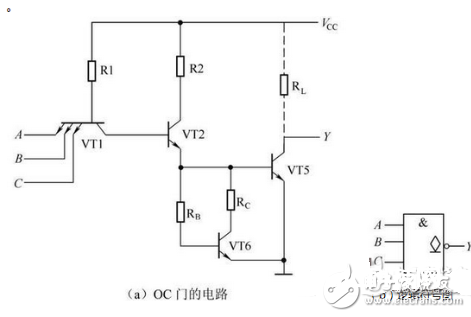
图2-20 集电极开路与非门及逻辑符号
② OC 门的使用。
OC门能够完结线与，如图2-21所示，逻辑表达式为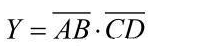
；驱动显示器、完结电平转化，如图2-22所示。
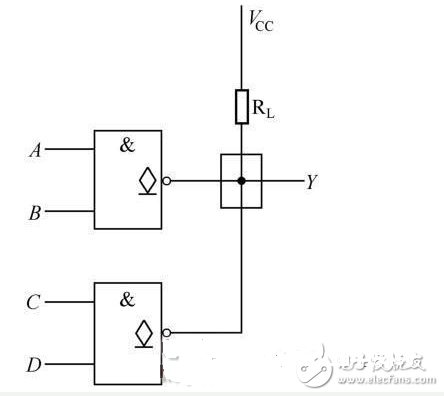
图2-21 用OC门完结线与
（3）与或非门
与或非门电路如图2-23（a）所示，逻辑符号如图2-23（b）所示，逻辑表达式为：
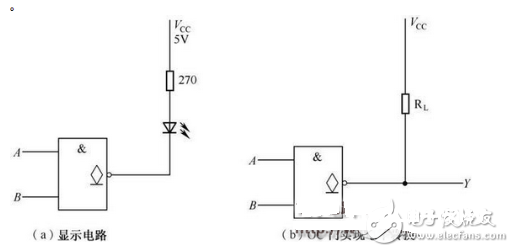
图2-22 驱动显示器、完结电平转化
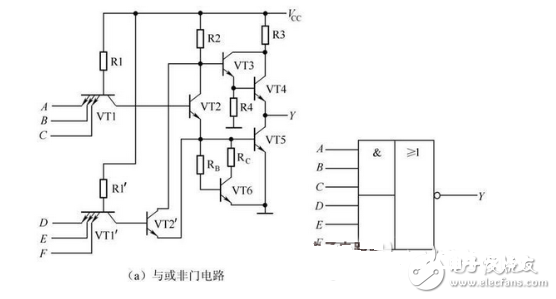
图2-23 与或非门及逻辑符号
（4）三态输出门
三态输出门是指不只可输出高电平、低电平两个状况，并且还可输出高阻状况的门电路，如图2-24所示，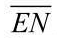
为操控端。
当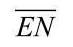
=0时，G输出P=1，VD截止，输出Y=
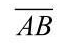，三态门处于作业状况。
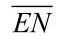低电平有用。
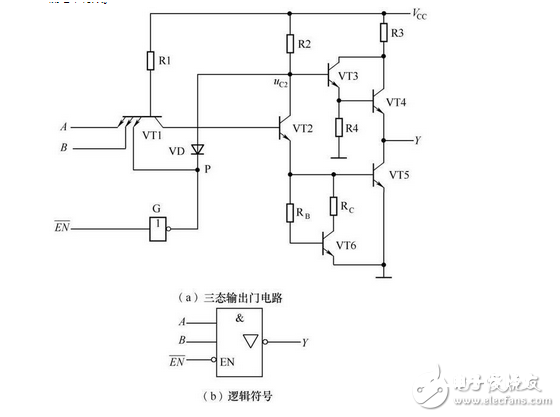
图2-24 三态输出与非门及其逻辑符号
当
=1时，G输出P=0，VD导通，输出高阻状况。
2．CMOS集成逻辑门
和 TTL 数字%&&&&&%比较，CMOS 电路的杰出特点是微功耗、高抗搅扰才能。
（1）CMOS反相器
由两个场效应管组成互补作业状况，如图 2-25 所示。逻辑表达式为：
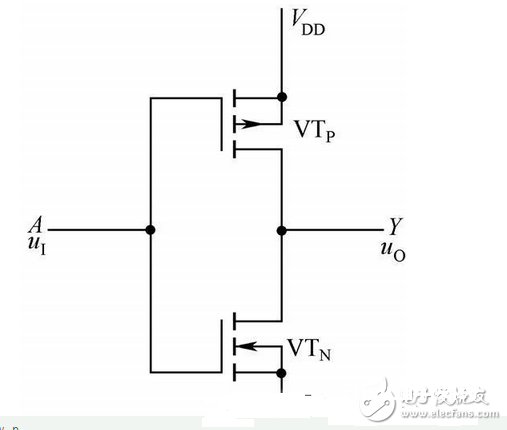
图2-25 CMOS 反相器
（2）CMOS与非门
如图2-26所示，两个串联的增强型NMOS管VTN1和VTN2为驱动管，两个并联的增强型PMOS管VTP1和VTP2为负载管，组成CMOS与非门，逻辑表达式为：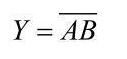
。
（3）CMOS或非门
如图2-27所示，两个并联的增强型NMOS管VTN1和VTN2为驱动管，两个串联的增强型PMOS管VTP1和VTP2为负载管，组成CMOS或非门，逻辑表达式为：
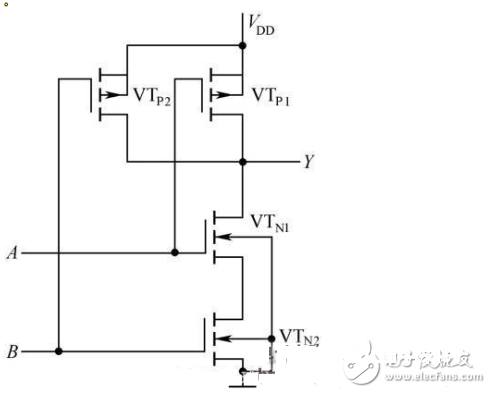
图2-26 CMOS 与非门
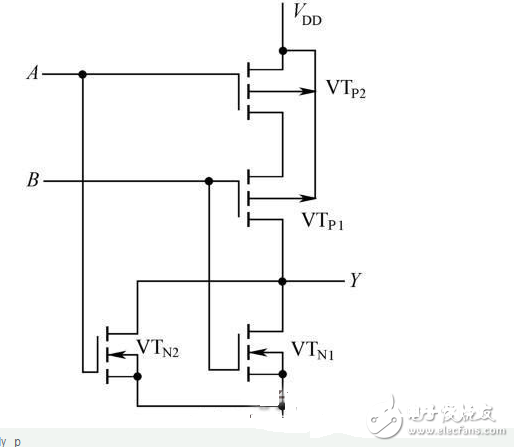
图2-27 CMOS 或非门
（4）CMOS传输门
将两个参数对称共同的增强型NMOS管VTN和PMOS管VTP并联可构成CMOS传输门，电路和逻辑符号如图2-28所示。
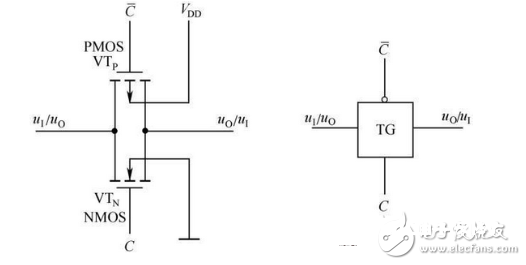
图2-28 CMOS 传输门及逻辑符号
（5）CMOS三态门
图 2-29（a）所示为低电平操控的三态门输出，图 2-29（b）为逻辑符号。
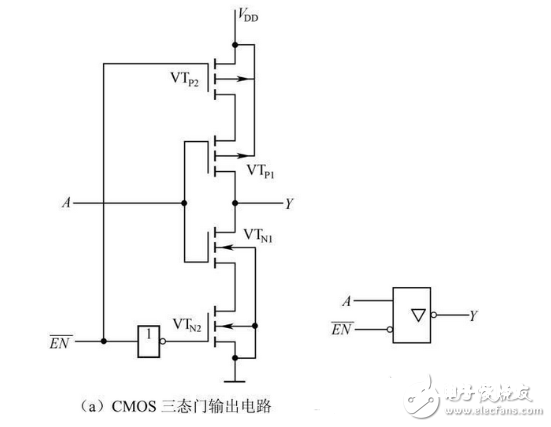
图2-29 CMOS 三态门输出及逻辑符号
当
时，VTP2和VTN2导通，VTN1和VTP1组成的CMOS反相器作业，所以
。
当
，VTP2和VTN2一起截止，输出Y对地和对电源VDD都呈高阻状况。
（6）CMOS异或门
图2-30（a）所示为异或门，图2-30（b）为逻辑符号。
图2-30 CMOS 异或门及逻辑符号
当输入A=B=0或A=B=1时，即输入信号相同，输出Y=0；当输入A=1或B=1时，即输入信号不同，输出Y=1。其真值表如表2-2所示。
表2-2 异或门真值表
3．复合门电路
除了上述介绍的逻辑门电路外，还有或非门、异或门、同或门等，表2-3是根本门和常用复合门的逻辑符号、逻辑表达式及逻辑功用。
表2-3 根本门和常用复合门的对照表
二、组合逻辑电路
逻辑电路在任何时间的输出状况只取决于这一时间的输入状况，而与电路的本来状况无关，则该电路称为组合逻辑电路。
1．组合逻辑电路的剖析办法
（1）剖析过程
① 依据给定的逻辑电路写出输出逻辑关系式。一般从输入端向输出端逐级写出各个门输出对其输入的逻辑表达式，然后写出整个逻辑电路的输出对输入变量的逻辑函数式。必要时，可进行化简，求出输出逻辑函数式。
② 列出逻辑函数的真值表。将输入变量的状况以天然二进制数次序的各种取值组合代入输出逻辑函数式，求出相应的输出状况，并填入表中，即得真值表。
③ 依据真值表和逻辑表达式对逻辑电路进行剖析，最终确认其功用。
（2）剖析举例
剖析图2-31所示逻辑电路的功用。
图2-31 逻辑电路
① 写出输出逻辑函数表达式：
② 列出逻辑函数的真值表。将输入A、B、C取值的各种组合代入式（2-5）中，求出输出Y的值。由此列出真值表，见表2-4。
表2-4 真值表
续表
③ 逻辑功用剖析。由表2-4可知：在输入A、B、C这3个变量中，有奇数个1时，输出Y为1，不然Y为0，由此可知，图2-34为这3位奇校验电路。
2．组合逻辑电路的规划办法
（1）规划过程
组合逻辑电路的规划，应以电路简略、所用器材最少为方针，其规划过程为：
① 剖析规划要求，列出真值表；
② 依据真值表写出输出逻辑函数表达式；
③ 对输出逻辑函数进行化简；
④ 依据最简输出逻辑函数式画逻辑图。
（2）规划举例
规划一个A、B、C3个人表决电路。当表决某个提案时，多数人赞同，提案通过，一起A具有否决权。用与非门完结。
① 剖析规划要求，列出真值表，见表2-5。设A、B、C赞同提案用1表明，不赞同用0表明，Y为表决成果，提案通过为1，通不过为0。
表2-5 真值表
续表
② 将输出逻辑函数化简，变换为与非表达式。由图 2-32 的卡诺图进行化简，可得
图2-32 卡诺图
将上式变化为与非表达式
③ 依据输出逻辑函数式（2-6）画逻辑图，如图2-33所示。
3．组合逻辑电路中的竞赛冒险
（1）竞赛冒险现象及其发生的原因
信号通过导线和门电路时，都存在时间的推迟，信号发生变化时也有必定的上升时间和下降时间。因而，同一个门的一组输入信号，通过不同数目的门，通过不同长度导线的传输，抵达门输入端的时间会有先有后，这种现象称为竞赛。
图2-33 逻辑电路
逻辑门因输入端的竞赛而导致输出发生不该有的尖峰搅扰脉冲（又称过渡搅扰脉冲）的现象，称为冒险。如图2-34所示。
图2-34 发生正尖峰搅扰脉冲冒险
（2）冒险现象的判别
在组合逻辑电路中，是否存在冒险现象，可通过逻辑函数来判别。假如依据组合逻辑电路写出的输出逻辑函数在必定条件下可简化成下列两种方式时，则该组合逻辑电路存在冒险现象，即：
例如，函数式
，在A=C=0时，
。若直接依据这个逻辑表达式组成逻辑电路，则或许呈现竞赛冒险。
（3）消除冒险现象的办法
①添加多余项。例如：
，当A=1，C=1时，存在着竞赛冒险。依据逻辑代数的根本公式，添加一项 AC，函数式不变，却消除了竞赛冒险，即
。
② 加封闭脉冲。在输入信号发生竞赛冒险时间内，引进一个脉冲将或许发生尖峰搅扰脉冲的门封闭住。封闭脉冲应在输入信号转化前到来，转化后消失。
③ 加选通脉冲。对输入或许发生尖峰搅扰脉冲的门电路添加一个接选通信号的输入端，只要在输入信号转化完结并安稳后，才引进选通脉冲将它翻开，此刻才答应有输出。
④ 接入滤波电容。假如逻辑电路在较慢速度下作业，能够在输出端并联一电容器。因为尖峰搅扰脉冲的宽度一般都很窄，因而用%&&&&&%即可吸收掉尖峰搅扰脉冲。
⑤ 修正逻辑规划。
三、时序逻辑电路
与组合逻辑电路不同，时序逻辑电路在任何一个时间的输出状况不只取决于其时的输入信号，并且还取决于电路本来的状况。
1．同步时序逻辑电路的剖析办法
（1）剖析过程
① 写方程式。写出时序逻辑电路的输出逻辑表达式（即输出方程）、各触发器输入端的逻辑表达式（即驱动方程）和时序逻辑电路的状况方程。
② 列状况转化真值表。将电路现状的各种取值代入状况方程和输出方程中进行核算，求出相应的次态和输出，然后列出状况转化真值表。
③ 逻辑功用的阐明。依据状况转化真值表来阐明电路的逻辑功用。
④ 画出状况图和时序图。
（2）剖析举例
剖析图 2-35 所示电路的逻辑功用，并画出状况转化图和时序图。
图2-35 待剖析逻辑电路图
① 写方程式：
输出方程：
驱动方程：
状况方程：将驱动方程式代入 JK 触发器的特性方程Qn+1=
，得到电路的状况方程为
②列状况转化真值表：该电路的现状为
，代入输出方程（2-9）和状况方程（2-11）中进行核算后得 Y=0 和
，然后再将001当作现态代入状况方程式（2-11），得
，以此类推。可求得可求得表2-6所示的状况转化真值表。
表2-6 状况转化真值表
③ 逻辑功用阐明：由表2-6可看出，图2-35所示电路在输入第六个计数脉冲CP，回来本来的状况，一起输出端Y输出一个进位脉冲。因而，该电路为同步六进制计数器。
图2-36 状况转化图和时序图
④ 画状况转化图和时序图。依据表2-6可画出图2-36（a）所示的状况转化图。图中的圆圈内表明电路一个状况，箭头表明状况转化方向，箭头线上方标示X/Y为转化条件，X为转化前输入变量的取值， Y为输出值，因为本例没有输入变量，故X未标上数值。
2．同步时序逻辑电路的规划办法
同步时序逻辑电路的规划和剖析正好相反，依据给定逻辑功用的要求，规划同步时序逻辑电路。规划的关键是依据规划要求确认状况转化的规则和求出各触发器的驱动方程。
