看到了一道关于旋转队伍的标题,觉得蛮有意思的,尽管仅仅是一个数值处理问题,可是寻觅规则的进程仍是蛮有意思的,关于旋转队伍的完成也已经有了许多的版别,我就其间的一种做扼要的剖析和总结。
标题大约如下所示:
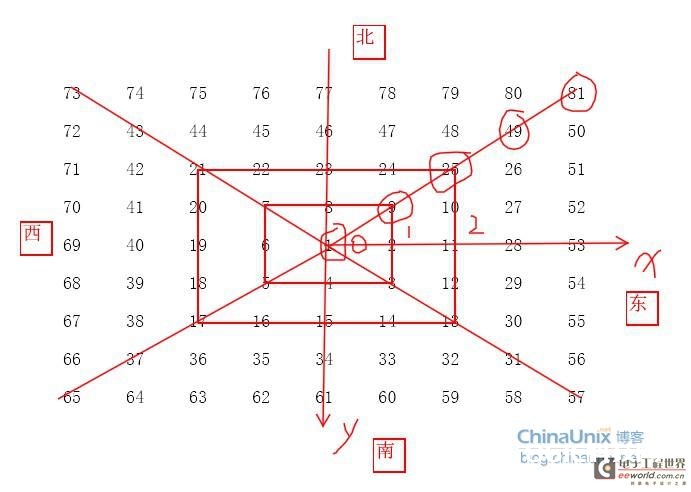
设1点的坐标是(0,0),x方向向右为正,y方向向下为正。例如:7的坐标为(-1,-1),2的坐标为(1,0),3的坐标为(1,1)。编程完成输入恣意一点坐标(x,y),输出所对应的数字;或输入恣意数字,输出该数字的坐标。完成的作用如上图所示,从图中可知,只需求找到正确的数值剖析式,就能够得到坐标处对应的数值。
下面扼要的剖析其间的一些规则,这类问题我觉得要害仍是要找到突破点,然后找到详细数值的表达式,表达式清楚了就仅仅程序的转化问题啦。
从图上可知,在第0层时只要一个值1,第1层是有8个值(2-9),第2层上的值从10到25,第3层的值从26到49,由图可知每一层的最终一个值都是奇数的平方(1,9,25,49,81,…),再和层数相关起来,得到每一层的最终一个数都是(2n+1)^2,相同每一层的开端值也就能够确认,即(2n-1)^2+1。也便是每一层的值都是处在(2n-1)^2+1和(2n+1)^2之间,这样选用(2n-1)^2作为一个基准,加上对应的数就能得到详细的数值。
因而咱们能够得到如下的定论:
旋转队伍每一层的开端值都是(2n-1)^2+1,完毕值都是(2n+1)^2,其间的n便是层数(0,1,2,…),能够认为是坐标中较大的绝对值值确认地点的层,比方(2,3),则表明该坐标处于第3层,而(-3,-2)也表明这个数值在第3层上。有了这种层的概念就会使得推理的进程更见的简略。也便是说坐标值中绝对值较大的值便是所谓的层。
结合上面的图画可知道,每一层的开端值都是出于东方,也便是x>0的方向,完毕于北方,即y<0的方向,这时候咱们能够根据东西南北四个方历来确认坐标对应的值。
即:首要选用输入的坐标值确认该数值对应的层数,然后根据输入坐标的x,y确认坐标地点的方向,这时候根据每一个方向的开端值就能较好的确认一切的值(详细剖析该值与每一层的开端值之间的联络),可是这种办法有问题,由于每一层上每个方向(东西南北)的开端坐标都是在改变的,并不便于得到通用的表达式。
这时候能够考虑对称性问题,由于在上面的图中咱们能够知道该图根本上是依照x,y对称的,假如咱们知道了四个正方向的值,那么就能根据对称性快速的确认其他的值,也便是只需求知道每一层与坐标轴相交的几个值就能快速的确认其他的值。
可是怎么让确认坐标轴上的值呢?
这就要密切联络每一层的完毕值(2n+1)^2,根据这个值咱们能够知道下一层正东方的值(2n+1)^2+n+1,参加坐标地点的层为K,则正东方的值就应该是(2*K-1)^2+K,这个能够很简单的确认,由于开端值到坐标轴的间隔刚好便是层数K,也便是加上K。其他三个方向的值也就能够快速的确认。
因而咱们能够知道每一个方向的对称轴的表达式分别为:
正东方:(2*K-1)^2+K
正南边:(2*K-1)^2+3K
正西方:(2*K-1)^2+5K
正北方:(2*K-1)^2+7K
根据每一个方向的坐标轴的对称性确认对应的值,在对称的方向上只需求一个坐标值就能确认其他的值,这时候四个方向上的值分别为:
东方:(2*K-1)^2 + K + y
南边:(2*K-1)^2 + 3K – x
西方:(2*K-1)^2 + 5K – y
北方:(2*K-1)^2 + 7K + x
这样也就找到了每一行的表达式,就能完成每一个方向上数值的确认。程序的完成也就相对来说十分简单完成啦。在打印的进程中需求留意数组队伍的不同。
完成的根本进程如下:
#include
#include
using namespacestd;
#define abs(x) ((x) > 0 ? (x) : (-x))
#define max(x,y) (abs(x) >= abs(y) ? abs(x) : abs(y))
int reverse_xy(int x, int y)
{
int cnt = 0;
/*保存地点的行*/
int t = max(x, y);
/*最早判别北方(y=-t)*/
if(-t == y)
{
cnt = (2*t-1)*(2*t-1) + 7*t + x;
}
else if(-t == x)/*西方*/
{
cnt = (2*t-1)*(2*t-1) + 5*t – y;
}
else if(t == y)/*南边*/
{
cnt = (2*t-1)*(2*t-1) + 3*t – x;
}
else if(t == x)/*东方*/
{
cnt = (2*t-1)*(2*t-1) + t + y;
}
return cnt;
}
int main()
{
int array[9][9] = {0};
int x = 0;
int y = 0;
for(y = 0; y <= 8 ; ++ y)
{
for(x = 0; x <= 8; ++ x)
{
array[x][y] = reverse_xy(x-4 , y-4);
cout << array[x][y] << " ";
}
cout << endl;
}
}