一、胶体理论
导致胶体粒子聚会的首要效果,是来自粒子间的范德华力,若要添加胶体粒子安稳性,则由两个途径,一是添加胶体粒子间的静电排挤力,二为使粉体间发生空间位阻,以这两种方法阻绝粉体的聚会。
最简略的胶体体系系由一涣散相与一相涣散前言所构成,其间涣散相标准规模于10-9~10-6m间。胶体内的物质存在于体系内需具有必定程度以上的涣散才能。依据溶剂与涣散相的不同而可发生多种不同的胶体型态,如:雾气即为液滴涣散于气体中之气胶、牙膏即固态高分子微粒涣散在液体中的溶胶。
胶体的使用在生活中举目皆是,而胶体的物理特性需视涣散相与涣散介质的不同而有所差异。从微观视点调查胶体,胶体粒子并非处于安稳状况,而是在介质内随机运动,这便是咱们所称的布朗运动(Brownian motion)。肯定零度以上,胶体粒子均会因热运动而发生布朗运动,这便是微观胶体的动力学特性。胶体粒子因布朗运动而发生磕碰,是为聚会(aggregate)发生的关键,而胶体粒子在热力学上处于不安稳状况,因而粒子间的交互效果力为涣散的关键因素之一。
1-1,胶体动力学性质
布朗运动起始自19 世纪初,植物学家布朗由显微镜调查到花粉粒子在水中的不规则运动得名。粒子因温度而构成布朗运动后将发生磕碰行为,由粒子外表的范德华力引起聚会现象。胶体的凝集速率与以下两者有亲近的联系:
1)胶体粒子间互相磕碰的频率,
2)粒子经磕碰后,发生的热能是否足以战胜胶体间的排挤能量。
Smoluchowski 提出胶体快速凝集理论,是由浓度差构成涣散速率所操控。
胶体粒子聚会的速率为:
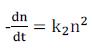
n表明在时刻t时,单位体积溶液所含的胶体粒子数,k2为二次反响速率常数(second-order rate constant)。
因为聚会使得溶液中的胶体粒子浓度削减,因而以表明为负号。当t=0,n=n0, 积分上式可得:

胶体部分聚会后,因为排挤能障将随粒子的粒径添加而生长,溶液将到达平衡,使得凝集速率下降。假定胶体粒子为单一粒径,并只考虑两粒子间的磕碰时:

a为胶体粒子半径,D为布朗涣散系数,假定为球形粒子,由爱因斯坦涣散规律,可得:
将(4)代入(3)后,n 代入(2)式化简得到:

K02为涣散速率拉制时的胶体凝集速率(不考虑能障时的速率常数),μf 为水溶液黏度。并由(1)及(5)式可计算出聚会时刻tF为:

1-2, 双电层理论
双电层理论可用以解说胶体中带电离子的散布景象,以及粒子外表所发生的电位问题。19 世纪Helmholtz 提出平行电容器模型以描绘双电层结构,简略的假定粒子带负电,且外表好像电容器中的电极,溶液中带正电的反离子因异电荷相吸而吸附在粒子外表。但是这个理论却疏忽了带电离子会因热运动发生涣散行为。
因而,在20世纪初Gouy与Chapman 提出涣散双电层模型,在溶液中的反离子会因静电效果吸附于带电粒子外表,一起受热运动影响而在粒子周围涣散。因而,反离子在溶液中的散布浓度将随粒子外表的间隔添加而下降。1924 年,史特恩(Stern)将平行电容器与涣散双电层两种模型加以结合,以描绘双电层结构。Stern以为反离子会在粒子外表构成严密的吸附层,亦称Stern layer,跟着与粒子外表间隔添加,粒子的电位会出现线性下降,一起Stern layer外亦有涣散层的存在,而且粒子于涣散层中的电位会随间隔添加而指数下降。
下图为Stern双电层模型,zeta电位(ξ,Zeta potential)为双电层模型中极重要的参数,实践丈量时并无法直接测得粒子的外表电位,但可由声波法或是电泳法计算出粒子的zeta电位。双电层模型中Stern 层与涣散层间的剪切平面上存在zeta电位。
zeta电位与胶体的涣散安稳性有亲近的联系,当zeta电位愈大时,胶体粒子外表上的静电荷愈多,当粒子于水溶液中的zeta电位到达±25~30mV 以上时,胶体有满足的静电排挤力战胜粒子间的范德华力以坚持胶体安稳性。

Stern 双电层模型
而胶体粒子外表的电荷来历有:
1)离子解离(Dissolution)
离子结晶型胶体粒子,组成离子具有不同的分化速率,发生外表电荷。离子与粒子外表和液相间的亲和性不同,也是粒子外表带电的原因之一。
2)离子化(Ionization)
当胶体外表具有额定的强酸碱、弱酸碱等官能基,如:羧酸或胺基等时,这此外表活性基会与溶液中的氢离子或氢氧根离子反响,发生如COO-、NH3+ 等使粒子外表带负电或正电。
3)离子吸附(Ion adsorption)
胶体外表的净电荷可由溶液中不同的离子吸附景象发生,导致粒子外表带过多的正电荷或负电荷。
4)电子亲和性(Electron affinities)
两相之间的电子亲和力不一起,会发生触摸电位(contact potential),使电荷别离。
5)缺点(Imperfection)
当粒子内部具有杂质时,例如:部份离子被同离子替代,不同价数的离子替代行为或许具有空位等缺点均会使粒子外表带有电荷。
6)偶极分子的吸附与取向性
胶体粒子外表吸附有偶极分子时,虽不影响胶体净电荷,但是将改动双电层中的电荷散布,使得电荷散布不均。粒子外表带电量将直接影响到胶体的安稳性。胶体外表的电荷会将反离子(Counter-ion)招引至粒子外表,而且排挤一起离子(Co-ion)。经由静电效果与热运动,反离子吸附于粒子外表,而过剩的一起离子则涣散于溶液里,构成了双电层的电荷散布。
二、DLVO理论
1940-1948年,由Deryagin、Landau、Verwey、Overbeek 树立胶体粒子互相挨近时的能量改变及对胶体安稳性影响的相关理论,简称DLVO理论。其理论首要描绘胶体粒子间隔与能量改变的联系,此效果能量是胶体双电层重迭的电荷排挤能与范德华力加成下的成果。
下图为DLVO示意图,表明胶体粒子之间存在招引力与排挤力,这两种效果力的巨细决议胶体溶液的安稳性,粒子间的招引力为首要效果,则粒子将发生聚会;而排挤力大于招引力的状况下,则可防止粒子凝集而坚持胶体的安稳性。
由DLVO曲线,当粒子之间的间隔愈来愈短,粒子首先会发生招引力,若粒子互相再继续挨近时,则将使得粒子之间发生排挤力,而若粒子跳过排挤能障,则会快速发生聚会。因而为了使得胶体内的粒子涣散安稳性进步,有必要进步粒子间排挤力,以防止粒子间发生聚会。

DLVO示意图
2-1,胶体的安稳机制
胶体粒子因为具有高外表能而倾向聚会状况,为使胶体体系具有涣散安稳性,有必要进步粒子间的排挤力。胶体间的安稳机制一般可分为三种:
1)静电安稳机制(Electrostatic stabilization)
2)立体妨碍(Steric hindrance)
3)静电立体安稳效果(Electrosteric stabilization),安稳机制如下图所示:

(a)静电斥力、(b)立体妨碍、(c)静电立体妨碍
静电安稳机制是使用粒子的外表电荷所构成的排挤力,当粒子互相因招引力挨近时,构成胶体粒子的双电层重迭,因为粒子外表带同性电荷,因而发生排挤力。
但是静电安稳机制易受溶液体系中的电解质浓度影响,当溶液内的电解质浓度过高时将构成粒子外表双电层紧缩,反而构成粒子的凝集。立体妨碍的安稳机制是使用高分子吸附于胶体粒子外表,其效果会发生两种不同的效应提高粒子间的排挤力:
1)渗透压效应(Osmotic Effect)
是当两胶体粒子挨近时,高分子长链吸附于粒子外表或溶液内的剩余高分子会介在粒子之间,此刻粒子间的高分子浓度不断进步将引起渗透压的改变,周围介质进入两粒子之间,排开互相间隔,而到达涣散安稳的效果。
2)空间约束效应(Volume restriction effect)
为吸附于粒上外表的高分子具有必定的空间阻止,当粒子间隔缩短,因为高分子并无法穿透粒子,高分子将发生紧缩,致使弹性自由能上升,因而排开粒子,到达涣散的效果。
相较于静电安稳机制,高分子立体妨碍具有许多长处。静电安稳机制极简略受环境影响而失掉效果,无法使用于高电解质环境或是有机体系溶液。
但是高分子立体妨碍对电解质浓度相对不灵敏,而且于水溶液或在有机溶剂中具有持平的功率,而且高分子立体妨碍亦不因胶体固含量而影响效果。高分子吸附于胶体粒子外表时,即便发生聚会亦为软聚会,可简略的破除聚会现象,即便胶体粒子通过枯燥程序,仍然是能够再度涣散于溶剂中。
因而立体妨碍关于涣散安稳性的效果相对较静电安稳效应高。静电立体安稳效果则是一起具有静电安稳机制与立体妨碍,粒子外表所接枝的高分子上带有电荷,使两种不同安稳机制加成,可让胶体粒子具有杰出的涣散安稳性。