作者从神经网络简略的数学界说开端,沿着丢失函数、激活函数和反向传达等办法进一步描绘根本的优化算法。在了解这些根底后,本文详细描绘了动量法等当时十分盛行的学习算法。此外,本系列将在后边介绍 Adam 和遗传算法等其它重要的神经网络练习办法。
I. 简介
本文是作者关于怎样「练习」神经网络的一部分经历与见地,处理神经网络的根底概念外,这篇文章还描绘了梯度下降(GD)及其部分变体。此外,该系列文章将在在后边一部分介绍了当时比较盛行的学习算法,例如:
动量随机梯度下降法(SGD)
RMSprop 算法
Adam 算法(自适应矩估量)
遗传算法
作者在榜首部分以十分简略的神经网络介绍开端,简略到仅仅满足让人了解咱们所议论的概念。作者会解说什么是丢失函数,以及「练习」神经网络或许任何其他的机器学习模型究竟意味着什么。作者的解说并不是一个关于神经网络全面而深度的介绍,现实上,作者期望咱们读者现已对这些相关的概念早已了然于心。假如读者想更好地了解神经网络详细是怎样运转的,读者能够阅览《深度学习》等相关书本,或参看文末供给的相关学习资源列表。
本文作者以几年前在 kaggle 上进行的猫狗辨别竞赛(https://www.kaggle.com/c/dogs-vs-cats)为例来解说一切的东西。在这个竞赛中咱们面对的使命是,给定一张图片,判别图中的动物是猫仍是狗。
II. 界说神经网络
人工神经网络(ANN)的发生受到了人脑作业机制的启示。虽然这种模仿是很不严厉的,可是 ANN 的确和它们生物意义上的创造者有几个类似之处。它们由必定数量的神经元组成。所那么,咱们来看一下一个独自的神经元吧。
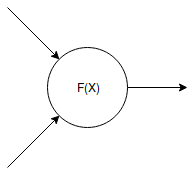
单个神经元
咱们接下来要议论的神经元是一个与 Frank Rosenblatt 在 1957 年提出的最简略的被称作「感知机,perception」的神经元略微有所不同的版别。我所做的一切修正都是为了简化,由于我在这篇文章中不会触及神经网络的深化解说。我仅仅试着给读者给出一个关于神经网络怎样作业的直觉知道。
什么是神经元呢?它是一个数学函数,并以必定量的数值作为输入(随意你想要多少作为输入),我在上图画出的神经元有两个输入。咱们将每个输入记为 x_k,这儿 k 是输入的索引。关于每一个输入 x_k,神经元会给它分配另一个数 w_k,由这些参数 w_k 组成的向量叫做权重向量。正是这些权值才使得每个神经元都是绝无仅有的。在测验的进程中,权值是不会改动的,可是在练习的进程中,咱们要去改动这些权值以「调理」咱们的网络。我会在后边的文章中评论这个内容。正如前面说到的,一个神经元便是一个数学函数。可是它是哪种函数呢?它是权值和输入的一种线性组合,还有根据这种组合的某种非线性函数。我会持续做进一步解说。让咱们来看一下首要的线性组合部分。

输入和权值的线性组合。
上面的公式便是我说到的线性组合。咱们要将输入和对应的权值相乘,然后对一切的成果求和。成果就会一个数字。终究一部分—便是给这个数字运用某种非线性函数。今日最常用的非线性函数即一种被称作 ReLU(rectified linear unit) 的分段线性函数,其公式如下:
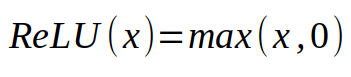
线性整流单元的表达式。
假如咱们的数字大于 0,咱们就会运用这个数字,假如它小于 0,咱们就会用 0 去替代它。这个被用在线性神经元上的非线性函数被称作激活函数。咱们有必要运用某种非线性函数的原因在后边会变得很明显。总结一下,神经元运用固定数目的输入和(标量),并输出一个标量的激活值。前面画出的神经元能够归纳成一个公式,如下所示:
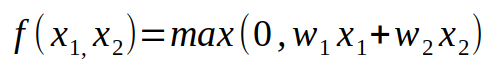
将我要写的内容略微提早一下,假如咱们以猫狗辨别的使命为例,咱们会把图片作为神经元的输入。或许你会疑问:当神经元被界说为函数的时分,怎样向它传递图片。你应该记住,咱们将图片存储在核算机中的办法是将它拿一个数组代表的,数组中的每一个数字代表一个像素的亮度。所以,将图片传递到神经元的办法便是将 2 维(或许 3 维的彩色图片)数组打开,得到一个一维数组,然后将这些数字传递到神经元。不幸的是,这会导致咱们的神经网络会依靠于输入图片的巨细,咱们只能处理由神经网络界说的某个固定巨细的图片。现代神经网络现已发现了处理这个问题的办法,可是咱们在这儿仍是在这个约束下规划神经网络。
现在咱们界说一下神经网络。神经网络也是一个数学函数,它便是许多相互衔接的神经元,这儿的衔接指的是一个神经元的输出被用为另一个神经元的输入。下图是一个简略的神经网络,期望用这张图能够将这个界说解说得愈加清楚。

一个简略的神经网络。
上图界说的神经网络具有 5 个神经元。正如你所看到的,这个神经网络由 3 个全衔接层堆叠而成,即每一层的每个神经元都衔接到了下一层的每一个神经元。你的神经网络有多少层、每一层有多少个神经元、神经元之间是怎样链接的,这这些要素一同界说了一个神经网络的架构。榜首层叫做输入层,包括两个神经元。这一层的神经元并不是我之前所说的神经元,从某种意义而言,它并不履行任何核算。它们在这儿仅仅代表神经网络的输入。而神经网络对非线性的需求源于以下两个现实:1)咱们的神经元是连在一同的;2)根据线性函数的函数仍是线性的。所以,假如不对每个神经元运用一个非线性函数,神经网络也会是一个线性函数罢了,那么它并不比单个神经元强壮。终究一点需求着重的是:咱们一般是想让一个神经网络的输出巨细在 0 到 1 之间,所以咱们会将它依照概率对待。例如,在猫狗辨别的比方中,咱们能够把挨近于 0 的输出视为猫,将挨近于 1 的输出视为狗。为了完结这个方针,咱们会在终究一个神经元上运用一个不同的激活函数。咱们会运用 sigmoid 激活函数。关于这个激活函数,你现在只需求知道它地返回值是一个介于 0 到 1 的数字,这正好是咱们想要的。解说完这些之后,咱们能够界说一个和上图对应的神经网络了。

界说一个神经网络的函数。w 的上标代表神经元的索引,下标代表输入的索引。
终究,咱们得到了某种函数,它以几个数作为输入,输出另一个介于 0 到 1 之间的数。实践上,这个函数怎样表达并不重要,重要的是咱们经过一些权重将一个非线性函数参数化了,咱们能够经过改动这些权重来改动这个非线性函数。
III. 丢失函数
在开端评论神经网络的练习之前,终究一个需求界说的便是丢失函数了。丢失函数是一个能够告知咱们,神经网络在某个特定的使命上表现有多好的函数。做这件事的最直觉的办法便是,对每一个练习样本,都沿着神经网络传递得到一个数字,然后将这个数字与咱们想要得到的实践数字做差再求平方,这样核算出来的便是猜测值与实在值之间的间隔,而练习神经网络便是期望将这个间隔或丢失函数减小。
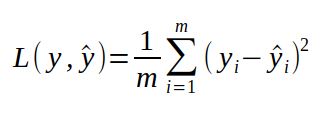
上式中的 y 代表咱们想要从神经网络得到的数字,y hat 指的一个样本经过神经网络得到的实践成果,i 是咱们的练习样本的索引。咱们仍是以猫狗辨别为例。咱们有一个数据集,由猫和狗的图片组成,假如图片是狗,对应的标签是 1,假如图片是猫,对应的标签是 0。这个标签便是对应的 y,在向神经网络传递一张图片的时分咱们想经过神经网络的得到的成果。为了核算丢失函数,咱们有必要遍历数据会集的每一张图片,为每一个样本核算 y,然后依照上面的界说核算丢失函数。假如丢失函数比较大,那么阐明咱们的神经网络功能并不是很好,咱们想要丢失函数尽或许的小。为了更深化地了解丢失函数和神经网络之间的联络,咱们能够重写这个公式,将 y 换成网络的实践函数。
IV. 练习
在开端练习神经网络的时分,要对权值进行随机初始化。明显,初始化的参数并不会得到很好的成果。在练习的进程中,咱们想以一个很糟糕的神经网络开端,得到一个具有高准确率的网络。此外,咱们还期望在练习完毕的时分,丢失函数的函数值变得特别小。提高网络是有或许的,由于咱们能够经过调理权值去改动函数。咱们期望找到一个比初始化的模型功能好许多的函数。
问题在于,练习的进程适当于最小化丢失函数。为什么是最小化丢失而不是最大化呢?成果证明丢失是比较简略优化的函数。
有许多用于函数优化的算法。这些算法能够是根据梯度的,也能够不是根据梯度的,由于它们既能够运用函数供给的信息,还能够运用函数梯度供给的信息。最简略的根据梯度的算法之一叫做随机梯度下降(SGD),这也是我在这篇文章中要介绍的算法。让咱们来看一下它是怎样运转的吧。
首要,咱们要记住关于某个变量的导数是什么。咱们拿比较简略的函数 f(x) = x 为例。假如还记得高中时分学过的微积分规矩,咱们就会知道,这个函数在每个 x 处的导数都是 1。那么导数能够告知咱们哪些信息呢?导数描绘的是:当我么让自变量朝正方向改动无限小的步长时,函数值改动有多快的速率。它能够写成下面的数学办法:

它的意思是:函数值的改动量(方程的左面)近似等于函数在对应的某个变量 x 处的导数与 x 的增量的乘积。回到咱们方才所举的最简略的比方 f(x) = x,导数处处是 1,这意味着假如咱们将 x 朝正方向改动一小步ε,函数输出的改动等于 1 和ε的乘积,刚好是ε自身。检查这个规矩是比较简略的。实践上这个并不是近似值,它是准确的。为什么呢?由于咱们的导数关于每一个 x 都是相同的。可是这并不适用于绝大多数函数。让咱们来看一个略微杂乱一点的函数 f(x) = x^2。

经过微积分常识咱们能够知道,这个函数的导数是 2*x。现在假如咱们从某个 x 开端移动某个步长的ε,很简略能够发现对应的函数增量并不准确地等于上面的公式中的核算成果。
现在,梯度是由偏导数组成的向量,这个向量的元素是这个函数所依靠的某些变量对应的导数。关于咱们现在所考虑的简略函数来说,这个向量只需一个元素,由于咱们所用的函数只需一个输入。关于愈加杂乱的函数(例如咱们的丢失函数)而言,梯度会包括函数对应的每个变量的导数。
为了最小化某个丢失函数,咱们能够怎样运用这个由导数供给的信息呢?仍是回到函数 f(x) = x^2。明显,这个函数在 x=0 的点取得最小值,可是核算机怎样知道呢?假定咱们开端的时分得到的 x 的随机初始值为 2,此刻函数的导数等于 4。这意味着假如 x 朝着正方向改动,函数的增量会是 x 增量的 4 倍,因而函数值反而会添加。相反,咱们期望最小化咱们的函数,所以咱们能够朝着相反的方向改动 x,也便是负方向,为了确保函数值下降,咱们只改动一小步。可是咱们一步能够改动多大呢? 咱们的导数只确保当 x 朝负方向改动无限小的时分函数值才会减小。因而,咱们期望用一些超参数来操控一次能够改动多大。这些超参数叫做学习率,咱们后边会谈到。咱们现在看一下,假如咱们从-2 这个点开端,会发生什么。这儿的导数是-4,这意味着假如朝着正方向改动 x,函数值会变小,这正是咱们想要的成果。
留意到这儿的规矩了吗?当 x>0 的时分,咱们导数值也大于 0,咱们需求朝着负方向改动,当 x<0 的时分,咱们导数值小于 0,咱们需求朝着正方向改动,咱们总需求朝着导数的反方向改动 x。让咱们对梯度也引证相同的思路。梯度是指向空间某个方向的向量,实践上它指向的是函数值添加最剧烈的方向。由于咱们要最小化咱们的函数,所以咱们会朝着与梯度相反的方向改动自变量。现在在咱们运用这个思维。在神经网络中,咱们将输入 x 和输出 y 视为固定的数。咱们要对其求导数的变量是权值 w,由于咱们能够经过改动这些权值类提高神经网络。假如咱们对丢失函数核算权值对应的梯度,然后朝着与梯度相反的方向改动权值,咱们的丢失函数也会随之减小,直至收敛到某一个部分极小值。这个算法就叫做梯度下降。在每一次迭代中更新权重的算法如下所示:
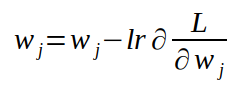
每一个权重值都要减去它对应的导数和学习率的乘积。
上式中的 Lr 代表的是学习率,它便是操控每次迭代中步长巨细的变量。这是咱们在练习神经网络的时分要调理的重要超参数。假如我么挑选的学习率太大,会导致步进太大,以至于越过最小值,这意味着你的算法会发散。假如你挑选的学习率太小,收敛到一个部分极小值或许会花费太多时刻。人们开发出了一些很好的技能来寻觅一个最佳的学习率,可是这个内容超出本文所触及的规模了。
不幸的是,咱们不能运用这个算法来练习神经网络,原因在于丢失函数的公式。
正如你能够在我之前的界说中看到的相同,咱们丢失函数的公式是和的均匀值。从微积分原理中咱们能够知道,微分的和便是和的微分。所以,为了核算丢失函数的梯度,咱们需求遍历咱们的数据会集的每一个样本。在每一次迭代中进行梯度下降是十分低效的,由于算法的每次迭代仅仅以很小的步进提高了丢失函数。为了处理这个问题,还有别的一个小批量梯度下降算法。该算法更新权值的办法是不变的,可是咱们不会去核算准确的梯度。相反,咱们会在数据集的一个小批量上近似核算梯度,然后运用这个梯度去更新权值。Mini-batch 并不能确保朝着最佳的方向改动权值。现实上,它一般都不会。在运用梯度下降算法的时分,假如所挑选的学习率满足小的话,能够确保你的丢失函数在每一次迭代中都会减小。可是运用 Mini-batch 的时分并不是这样。你的丢失函数会跟着时刻减小,可是它会有动摇,也会具有更多的「噪声」。
用来估量梯度的 batch 巨细是你有必要挑选的另一个超参数。一般,咱们期望尽或许地挑选能处理的较大 batch。可是我很少见到他人运用比 100 还大的 batch size。
mini-batch 梯度下降的极点状况便是 batch size 等于 1,这种办法的梯度下降叫做随机梯度下降(SGD)。一般在许多文献中,当人们说随机梯度下降的时分,实践上他们指的便是 mini-batch 随机梯度下降。大多数深度学习结构都会让你挑选随机梯度下降的 batch size。
以上是梯度下降和它变体的根本概念。但近来越来越多的人在运用更高档的算法,其间大多数都是根据梯度的,作者下一部分就首要介绍这些最优化办法。
VII. 反向传达(BP)
关于根据梯度的算法,剩余的仅有一件事便是怎样核算梯度了。最快速的办法便是解析地给出每一个神经元架构的导数。我想,当梯度遇到神经网络的时分,我不该该说这是一个张狂的主意。咱们在前面界说的一个很简略的神经网络就现已适当艰难了,而它只需戋戋 6 个参数。而现代神经网络的参数动辄便是数百万。
第二种办法便是运用咱们从微积分中学到的下面的这个公式去近似核算梯度,现实上这也是最简略的办法。
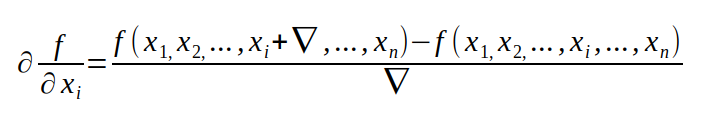
虽然这个办法是十分简略完结的,可是它却是十分耗核算资源的。
终究一种核算梯度的办法,是对解析难度和核算成本的折中,这个办法被称作反向传末节。反向传达不在本文的评论规模,假如你想了解更多的话,能够检查 Goodfellow《深度学习》第六章第五末节,该章节对反向传达算法有十分翔实的介绍。
VI. 它为什么会起作用?
当我初度了解神经网络以及它是怎样作业的时分,我了解一切的方程,可是我不是十分确认它们为啥会起作用。这个主意对我而言有些荒诞:用几个函数,求一些导数,终究会得到一个能够认出图片中是猫仍是狗。为什么我不能给你们一个很好的关于为啥神经网络会如此好的见效的直觉常识呢?请留意以下两个方面。
1. 咱们想要用神经网络处理的问题有必要被以数学的办法表达出来。例如,关于关于猫狗辨别:咱们需求找到一个函数,它能够把一副图片中的一切像素作为输入,然后输出图片中的内容是狗的概率。你能够用这种办法去界说任何一个分类问题。
2. 或许并不是很清楚,为什么会有一个能够从一副图片中把猫和狗区别开来的函数。这儿的思维是:只需你有一些具有输入和标签的数据集,总会存在一个能够在一个给定数据集上功能杰出的函数。问题在于这个函数会适当杂乱。这时分神经网络就能够有所协助了。有一个「泛迫临性原理,universal approximation theorem」,指的是具有一个躲藏层的神经网络能够近似任何一个你想要的的函数,你想要它近似得多好,就能有多好。
动量随机梯度下降算法
-这是关于练习神经网络和机器学习模型优化算法系列的第二部分,榜首部分是关于随机梯度下降的。在这一部分,假定读者对神经网络和梯度下降算法已有根本了解。假如读者对神经网络一窍不通,或许不知道神经网络是怎样练习的,能够在阅览这部分之前阅览榜首部分。
在本节中,除了经典的 SGD 算法外,咱们还会对动量法进行评论,这种算法一般比随机梯度下降算法更好更快。动量法 [1] 或具有动量的 SGD 是一种办法,这种办法有助于加快向量向着正确的方向梯度下降,然后使其收敛速度更快。这是最盛行的优化算法之一,许多各方向上最先进的模型都是用这种办法进行练习的。在讲高档的算法相关方程之前,咱们先来看一些有关动量的根底数学常识。
指数加权均匀
指数加权均匀用于处理数字序列。假定咱们有一些喧闹的序列 S。在这个比方中,我制作了余弦函数并添加了一些高斯噪声。如下图所示:
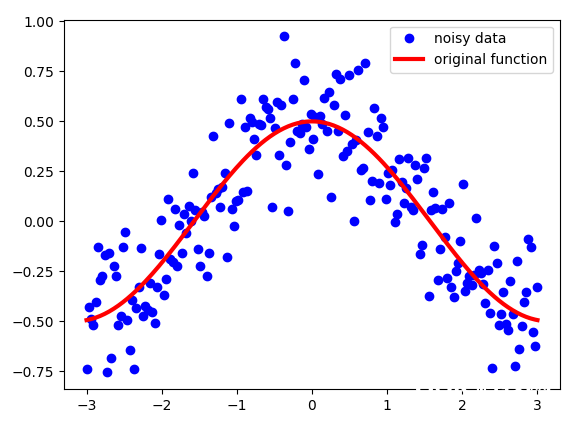
留意,虽然这些点看起来十分挨近,但它们的 x 坐标是不同的。也便是说,对每个点而言,其 x 坐标是仅有的标识,因而这也是界说序列 S 中每个点的索引。
咱们需求处理这些数据,而非直接运用它们。咱们需求某种「移动」的均匀值,这个均匀值会使数据「去噪」然后使其更挨近原始函数。指数加权均匀值能够发生如下所示的图片:

动量——来自指数加权均匀的数据
如咱们所见,这是一个适当不错的成果。与噪声很大的数据比较,咱们得到了更滑润的曲线,这意味着与初始数据比较,咱们得到了与原始函数更挨近的成果。指数加权均匀值用下面的公式界说了新的序列 V:
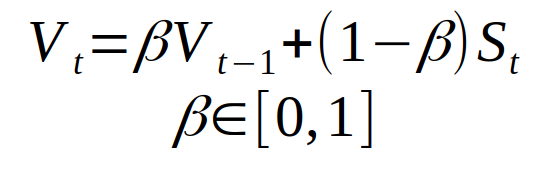
序列 V 是上面的散点图中的黄色部分。Beta 是取值为 0 到 1 的另一个超参数。在上述比方中,取 Beta = 0.9。0.9 是一个很好的值,常常用于具有动量的 SGD 办法。咱们能够这样对 Beta 进行直观了解:咱们对序列后边的 1 /(1- beta)的点进行近似均匀。让咱们看看 beta 的挑选会对新序列 V 发生怎样的影响。

Beta 取值不一同的指数加权均匀成果。
如咱们所见,Beta 取值越小,序列 V 动摇越大。由于咱们均匀的比方更少,因而成果与噪声数据更「挨近」。跟着 Beta 值越大,比方当 Beta = 0.98 时,咱们得到的曲线会愈加油滑,可是该曲线有点向右偏移,由于咱们取均匀值的规模变得更大(beta = 0.98 时取值约为 50)。Beta = 0.9 时,在这两个极点间取得了很好的平衡。
数学部分
这个部分对你在项目中运用动量而言不是必要的,所以能够越过。但这部分更直观地解说了动量是怎样作业的。
让咱们对指数加权均匀新序列 V 的三个接连元素的界说进行扩展。
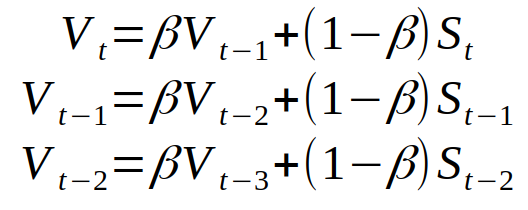
V——新序列。S——原始序列。
将其进行兼并,咱们能够得到:
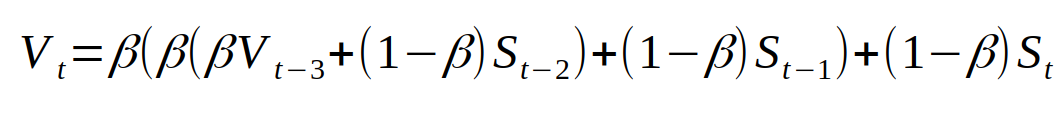
再对其进行简化,可得:
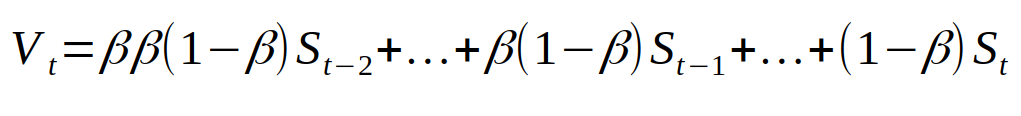
从这个等式中能够看出,新序列的第 T 个值取决于原始序列 S 的一切从前的数值 1…t。来自 S 的一切数值被赋了必定的权重。这个权重是序列 S 的第(t-i)个值乘以(1- beta)得到的权重。由于 Beta 小于 1,所以当咱们对某个正数的幂取 beta 时,值会变得更小。所以序列 S 的原始值的权重会小得多,也因而序列 S 对序列 V 发生的点积影响较小。从某些视点来说,该权重小到咱们简直能够说咱们「忘掉」了这个值,由于其影响小到简直无法留意到。运用这个近似值的长处在于当权重小于 1 / e 时,更大的 beta 值会要求更多小于 1 / e 的权值。这便是为什么 beta 值越大,咱们就要对更多的点积进行均匀。下面的图表显现的是与 threshold = 1 / e 比较,跟着序列 S 初始值改动,权重变小的速度,在此咱们「忘掉」了初始值。

终究要留意的是,榜首次迭代得到的均匀值会很差,由于咱们没有满足的值进行均匀。咱们能够经过运用序列 V 的误差修正版而不是直接运用序列 V 来处理这一问题。
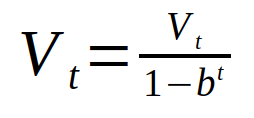
式中 b = beta。当 t 值变大时,b 的 t 次幂与零无法进行区别,因而不会改动 V 值。可是当 t 取值较小时,这个方程会发生较好的成果。可是由于动量的存在使得机器学习进程安稳得很快,因而人们一般会懒得运用这一部分。
动量 SGD 法
咱们现已界说了一种办法来取得一些序列的「移动」均匀值,该值会与数据一同改动。咱们该怎样将其运用于神经网络的练习中呢?它能够均匀咱们的梯度。我将在下文中解说它是怎样在动量中完结的这一作业,并将持续解说为什么它或许会得到更好的作用。
我将供给两个界说来界说具有动量的 SGD 办法,这简直便是用两种不同的办法表达同一个方程。首要,是吴恩达在 Coursera 深度学习专业化(https://www.deeplearning.ai/)的课程中提出的界说。他解说的办法是,咱们界说一个动量,这是咱们梯度的移动均匀值。然后咱们用它来更新网络的权重。如下所示:

式中 L 是丢失函数,三角形符号是梯度 w.r.t 权重,α 是学习率。另一种最盛行的表达动量更新规矩的办法不那么直观,仅仅省掉了(1 – beta)项。

这与榜首组方程式十分类似,仅有的区别是需求经过(1 – β)项来调整学习率。
Nesterov 加快突变
Nesterov 动量是一个版别略有不同的动量更新,最近越来越受欢迎。在这个版别中,首要会得到一个当时动量指向的点,然后从这个点核算梯度。如下图所示:

Nesterov 动量可用下式界说:

动量作业原理
在这儿我会解说为什么在绝大多数状况下动量法会比经典 SGD 法更好用。
运用随机梯度下降的办法,咱们不会核算丢失函数的切当导数。相反,咱们是对一小批数据进行预算的。这意味着咱们并不总是朝着最佳的方向行进,由于咱们得到的成果是「喧闹的」。正如我在上文中列出的图表。所以,指数的加权均匀能够供给一个更好的估量值,该估量值比经过喧闹核算得到的成果更挨近实践值的导数。这便是动量法或许比传统 SGD 更好的原因之一。
另一个原因在于沟谷(ravine)。沟谷是一个区域,在其间,曲线在一个维度比另一个维度陡得多。在深度学习中,沟谷区可近似视为部分最低点,而这一特性无法用 SGD 办法得到。SGD 倾向于在狭隘的沟谷上摇摆,由于负梯度将沿着峻峭的一侧下降,而非沿着沟谷向最长处行进。动量有助于加快梯度向正确的方向行进。如下图所示:

左图——没有动量的 SGD,右图——有动量的 SGD(来历:https://www.willamette.edu/~gorr/classes/cs449/momrate.html)
定论
期望本节会供给一些关于具有动量的 SGD 办法是怎样起作用以及为什么会有用的主意。实践上它是深度学习中最盛行的优化算法之一,与更高档的算法比较,这种办法一般被人们更频频地运用。
参阅资源
fast.ai(http://fast.ai/) :它针对程序员供给了两个很不错的关于深度学习的课程,以及一个关于可核算线性代数的课程。是开端编写神经网络代码的好地方,跟着课程深度的延伸,当你学到更多理论的时分,你能够赶快用代码完结。
neuralnetworksanddeeplearning.com(http://neuralnetworksanddeeplearning.com/chap1.html):一本关于根本常识的很好的在线书本。关于神经网络背面的理论。作者以一种很好的办法解说了你需求知道的数学常识。它也供给并解说了一些不运用任何深度学习结构从零开端编写神经网络架构的代码。
Andrew Ng 的深度学习课程(https://www.coursera.org/specializations/deep-learning):coursera 上的课程,也是有关学习神经网络的。以十分简略的神经网络比方开端,逐渐到卷积神经网络以及更多。
3Blue1Brown(https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw):YouTube 上也有一些能够协助你了解神经网络和线性代数的很好的视频。它们展现了很棒的可视化办法,以及以十分直觉的办法去了解数学和神经网络。
Stanford CS231 课程(http://cs231n.stanford.edu/):这是关于用于视觉辨认的卷积神经网络的讲堂,能够学到许多关于深度学习和卷积神经网络的详细内容。
参阅文献
[1] Ning Qian. On the momentum term in gradient descent learning algorithms . Neural networks : the official journal of the International Neural Network Society, 12(1):145–151, 1999
[2] Distill, Why Momentum really works(https://distill.pub/2017/momentum/)
[3] deeplearning.ai
[4] Ruder(2016). An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747
[5] Ruder (2017) Optimization for Deep Learning Highlights in 2017.(http://ruder.io/deep-learning-optimization-2017/index.html)
[6] Stanford CS231n lecture notes.(http://cs231n.github.io/neural-networks-3/)(http://cs231n.github.io/neural-networks-3/%EF%BC%89)
[7] fast.ai(http://www.fast.ai/)