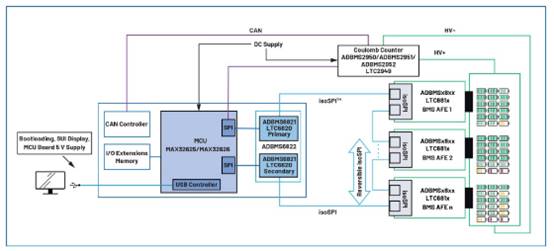
7.1.3 虹膜外边际的确认
(1) 虹膜外边际的特征剖析
由图1中所示的虹膜图画能够看出,虹膜外边际的首要特点是:较相对与虹膜内边际而言,边际处灰度改变不是特别显着,有一小段突变的区域。也就是说,虹膜内部灰度趋近于共同这个现实,在参考文献[8]中,介绍的环量积分算子应该式是一种有用的办法。
即:
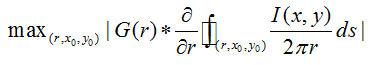
(7-10)
(2) 选用环量积分算子完成虹膜外边际的检测
如上剖析,虹膜环量积分算子是检测虹膜外边际的一种有用手法,为了战胜虹膜纹路对环量线积分的影响,本文对式(7-1)作了如下改善,将环量线积分
改变为求
的圆环状区域的面积分。即:
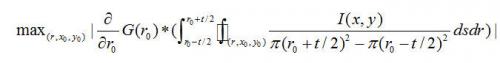
(7-11)
各符号的含义与(7-1)相同,为了便于核算,将其离散化可得:

(7-12)
式中
分别为t,
增加的步长,n,k,l,m分别为求卷积时高斯函数的中心、圆环中心、圆环的宽度、旋转视点等参数的增量。清楚明了,式(7-12)和式(7-11)并不彻底等价,式(7-11)中积分号内的部分的含义为积分区域内各个点的灰度的平均值,式(7-12)核算的是积分区域各个点灰度的总和,但因为(7-12)中视点
的步长
和圆环宽度t 的步长
以及圆环的宽度t 都是固定的,也就是说,对应不同的的圆环,从其间提取的核算环量积分的点的个数都是固定的,因而两者只相差一个份额常数,并不影响判别。留意,由式(7-1)到式(7-11)的改善进程顶用到了卷积的性质:
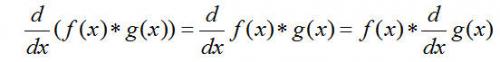
(7-13)
假如运用式(7-12)在整个图画空间中查找,则体系开支过大,本文将充分运用现已求得的瞳孔中心的方位参量,设定虹膜外边际的圆心与瞳孔中心相差5 各像素,然后将在整个区域内的查找简化为在5×5 的矩形区域内的查找,大大削减了算法的时刻复杂度。考虑到虹膜图画的上部和下部易于遭到眼皮和睫毛的搅扰,在核算环量积分时,
取值限定在
的范围内。
为了进一步削减体系查找的开支,本文选用一种由粗到精的取点与核算办法,设点
为查找点,以t 为半径增量,顺次核算式(7-11)所示的环量面积分算子,在查找空间内求得经过环量面积分的的最大值开始确认圆心和半径
之后,再以
为圆心,在
区域内运用式(7-1)准确查找,以确认圆的准确巨细。
7.2 虹膜图画的打开
为了便于对虹膜图片剖析,一般的体系中都要将其打开成矩形。
咱们选用内圆圆心为中心,以虹膜的宽度为半径树立极坐标系,将虹膜在极坐标系(ρ,θ)下打开成为横坐标为θ,纵坐标为ρ的720*50 的矩形区域,打开的进程中,必然会呈现新的图画中某些点无法与原图画中的点进行匹配的状况,一般状况下应进行插值处理,一般状况下,插值有以下几种办法:(1)0级内插法,即将该点周围四个邻点中离它最近的一个点的像素的灰度级做为它的灰度级。(2)1 级内插法,亦称双线性内插法,是根据周围四个点的灰度在两个方向上进行线性内插,然后对原图画中不存在的点核算出其近似值而不是用其附近点的像从来替代。(3)三次卷积法,是运用多项式来迫临理论上的最佳插值函数
的办法。因为0 级插值法缺少必定的精度,而三次卷积法又核算量过大,本文中采纳双线性内插法。运用极坐标的长处是:眼睛旋转的改变,能够转变为θ方向的平移。
7.3 虹膜图画的二值化
如上文所述,虹膜外表有许多斑驳、洼陷区和皱纹组成,这些特征构成与遗传和胚胎发育进程,含有丰厚的信息。并且毕生不变,从这些信息中能够用不同视点用不同的办法提取出用于区别不同虹膜的特征,然后进行身份辨认。
本文选用虹膜图画的结构特征剖析办法进行虹膜辨认。结构特征一般包含控制点,角,线段等等,结构特征具有直观性好、稳定性高、抗噪声能力强、编码功率高级长处。运用结构特征进行编码能够方便地处理虹膜图画残损问题和部分编码的区域区分差错。因为结构特征的直观性,便于构成一致的数据格式,有利于使用的推行。在灰度图中,虹膜区域的纹路特征表现为虹膜区域内的灰度改变,记载这些灰度改变,对图画进行二值化处理,将图画布景和灰度急剧改变的区域分隔,能够作为虹膜辨认的根据,下面就讨论虹膜图画二值化的办法。
7.3.1 虹膜图画二值化办法讨论
从直观来看,提取图画灰度改变的办法只需设定必定的阈值就提取其改换的信息,可是这种办法在提取灰度改变信息时却有必定的局限性。如图9所示为一图画的截面图。横坐标表明截面的扩展方向,纵坐标表明对应点的灰度,若取阈值为A,则BC的之间的灰度改变表现不出来,同理,若取阈值为C,则无法表现AB之间的阈值改变。
7.3.2 边际检测与滤波器的挑选
关于灰度图画中的各点,其灰度值的一阶或二阶导数能够很好地表现图画边界点,本文将讨论用二阶导数来求边际点,以反映图画灰度的改变,然后确认特征点,可是因为噪声信号的影响,一般应先对信号进行滑润滤波,设信号g(x),如滑润滤波器的冲击响应函数用h(x)表明,则滤波后的信号为g(x)=f(x)*h(x),然后再对g(x)求二阶导数以检测边际点。
因为微分运算与卷积运算次第有以下交换联系:
因而能够先滑润,后微分的两步运算兼并,并将滑润滑润微分滤波器的导数称为一阶微分滤波器,将
称为二阶微分滤波器,滑润滤波器应满意以下条件:
(1)当
为偶函数;
(2)
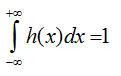
;
(3)h(x)一阶及两阶可微;
上述第二个条件确保了信号经滑润滤波器h(x)滤波之后,其均值不变。
Marr 提出用下述的高斯函数作为滑润滤波器: