引 言
在传感器非线性校对范畴,国内外许多学者提出多种办法,并得到广泛使用,传统办法归纳起来可分两类:一类是公式法,即以试验数据为根底,用最小二乘等体系辨识办法求取拟合曲线参数,树立校对曲线的解析表达式;另一类是表格法,以查表为手法,经过分段线性化来迫临传感器的非线性特性曲线。
近些年来,跟着神经网络的开展,又有不少学者使用神经网络的非线性回归才能,拟合传感器输出与输入的非线性联系,树立传感器传输特性的逆模型,从而使传感器亦即神经网络构成的体系线性化。可是,该办法也存在必定的局限性,首要表现在:1)神经网络存在部分极小和过学习问题,易影响网络的泛化才能,因而,对样本的数量和质量依靠强;2)网络练习成果与网络初值、样本次第等有关,所建逆模型不具备唯一性;3)一般不能给出非线性校对环节(逆模型)的数学解析表达式。
本文在前人研讨的根底上,将现代办法与传统办法相结合,提出一种使用最小二乘支撑向量机(least squares support vector machine,LS-SVM)的回归算法/辨识传感器非线性逆模型的新办法,最终,经过铂铑30-铂铑6热电偶(B型)非线性校对实例,验证了上述定论。
1、传感器非线性校对原理
大多数传感体系都可用y=f(x),x∈(ξa,ξb)标明,其间,y标明传感体系的输出,x标明传感体系的输入,ξa,ξb为输入信号的规模。y信号可经过电子设备进行丈量,但通常是依据测得的y信号求得不知道的变量x,即标明为x=f-1(y)。但在实践使用过程中,绝大多数传感器传递函数为非线性函数。
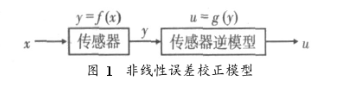
为了消除或补偿传感体系的非线性特性,可使其输出y,经过一个补偿环节,如图1所示。该模型的特性函数为u=g(y),其间,u为非线性补偿后的输出,它与输入信号x呈线性联系,并使得补偿后的传感器具有抱负特性。很显着,函数g(·)也是一个非线性函数,若其输入-输出联系刚好为传感器传输特性的逆映射,那么,就可以使补偿成果u在数值上与被测物理量共同。
实践上,热电偶在整个丈量规模的非线性联系可用分度表标明,可是,在实践进行非线性校对时,构建补偿环节需求的是温度对热电动势的分度函数联系t(E),即需求依据热电动势来反求相应的温度值。可用一个幂级数多项式来拟合温度对热电动势的非线性联系,并作为传感器非线性补偿器的数学模型,这样,不光便于核算,一起,也具有通用性。很显着,多项式的次数越高,拟合的精度也就越高,非线性校对的作用也越抱负;当然,进行线性化校对时的核算量也随之上升,因而,在实践使用时应权衡考虑。
无妨设补偿器分度函数具有如下方式

从上述剖析来看,对传感器非线性进行校对的关键在于:构建如式(2)或式(3)所示的补偿器模型,对其进行辨识,并求取参数ω与6。因而,可采用体系辨识办法结构温度传感器非线性补偿环节(逆模型),具体步骤如下:


2、 LS-SVM体系辨识原理



3 、实践传感器校对试验
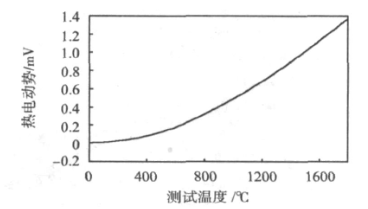
铂铑30-铂铑6热电偶(B型)在0~1 820℃规模内的输入-输出特性如图3所示,在低温段有较严峻的非线性,直接影响丈量精度,有必要添加非线性补偿环节进行校对使其线性化。

将该数学模型串联在铂铑30-铂铑6热电偶(B型)的输出端,可构成具有非线性自校对功用的传感器体系,经过该校对模型之后,使热电偶体系的线性度由校对之前的0.2123降为0.0353,体系的输入-输出特性如图4所示。

值得注意的是,铂铑30-铂铑6热电偶(B型)在整个测验规模中的传输特性曲线并不是单调递加的。因为在0~100℃段,传感器的分度函数出现U型散布,例如:与输出热电动势E=0 mV对应的测验温度可能是0℃,也可能是40℃。所以,在低温段,该传感器传递函数的反函数是不存在的,影响了该部分非线性校对的作用;但在中高温段(400~1800℃)传感器输出的具有显着的单调特性,因而,在该温度段用逆模型进行校对取得了适当抱负作用。图4所示的实践校对成果也标明:除低温段外,传感器体系的校对值与实在值十分挨近。
4、 结束语
经过构建传递函数的逆模型可完成传感器的非线性校对,进步传感器的丈量精度。本文针对实践问题,树立幂级数多项式补偿模型,并使用LS-SVM的回归算法辨识模型参数,完成传感器的非线性校对。
本文办法是现代技能(人工智能)和传统办法(最小二乘法)的一种结合,与神经网络为代表的人工智能办法不同,本文办法并没有使用非线性学习才能迫临模型的输入-输出特性;而是使用LS-SVM线性回归算法进行模型参数辨识,因而,可给出补偿器模型的解析方式数学表达式。最终,实践铂铑30-铂铑6热电偶(B型)非线性校对实例验证了本文办法的可行性。
责任编辑:gt