1.滤波电路的的类型及各类型的优缺陷。
1.1巴特沃斯型(Butterworth)
长处:通频带内的频率呼应曲线最大极限平整,没有崎岖。
缺陷:阻频带衰减较缓。
1.2切比雪夫型(Chebyshev)
长处:通频带内的频率呼应曲线不如巴特沃斯平整。
缺陷:阻频带衰减较快。
1.3贝塞尔型(Bessel)
长处:最大平整的群推迟(线性相位呼应)的线性过滤器,常用在音频天桥体系中。
2.滤波电路的规划(以巴特沃斯型低通为例)
滤波电路规划触及两个参数:截止频率、阶数
举例:规划一个到频率在75Hz,到150Hz衰减为30dB的巴特沃斯型低通滤波器
过程一:确认阶数,依据下图
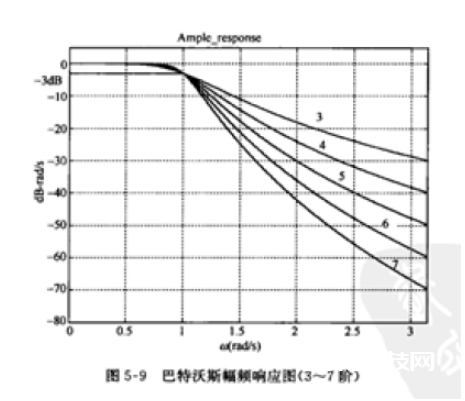
依据公式:a = W1(最大衰减频率)/W2(到频率)
a = 150Hz/75Hz = 2;
当a = 2,衰减倍数为30dB,依据上图,得阶数为5阶。
过程二:确认阶数的电路结构
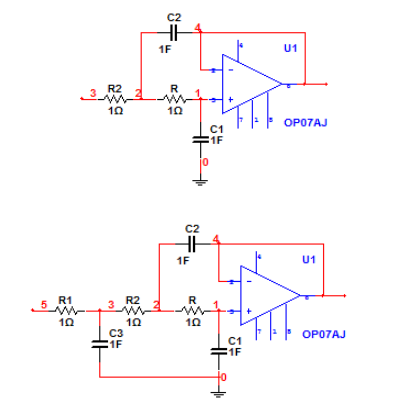
二阶节 三阶节
依据过程一算出的阶数:5 = 2 + 3 ;(假设4阶便是2 + 2)。
5阶就等于上图的二阶节与三阶节的拼接。
过程三:确认参数
解归一化:①先确认R = Z = 50K ;(频率低阻值大点,频率阻值小点)
②依据公式:FSF = 2π*f (f为到频率)
FSF = 2π * 75 = 471
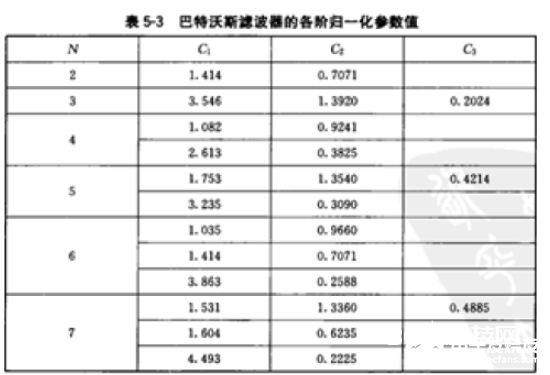
③确认电容:依据上图表中的数据
C1= 1.7530/(FSF*Z) = 74 nF
C2= 1.3540/(FSF*Z) = 57 nF
C3= 0.4214/(FSF*Z) = 18 nF
C4= 3.2350/(FSF*Z) = 137 nF
C5= 0.3090/(FSF*Z) = 13 nF
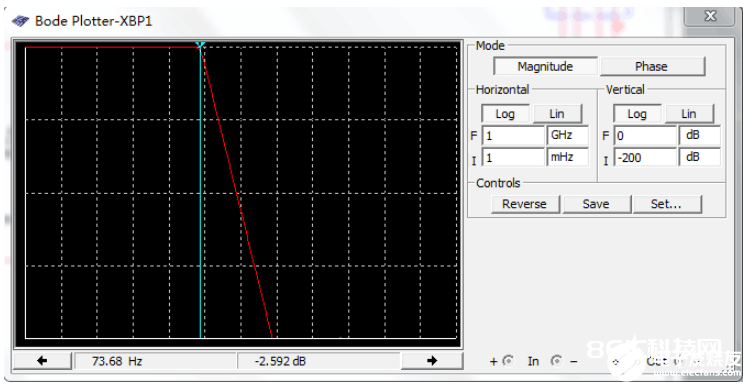
终究成果,如下图:
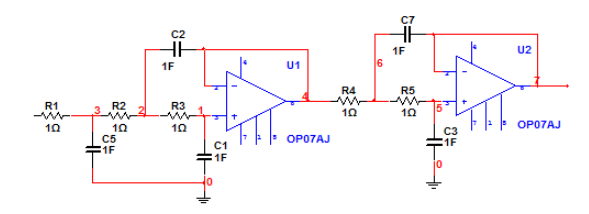
Multisim仿真成果: