脑部MR图画的Sigma-IFCM切割算法剖析

图画切割是把图画切割成互不相交的区域，使每个区域内的像素具有某种类似的特征，以便对图画进行后续处理。图画切割是图画剖析的难点之一，至今没有一个通用且有用的图画切割办法能够满意不同的需求。在脑部MR图画剖析中该问题尤为杰出。

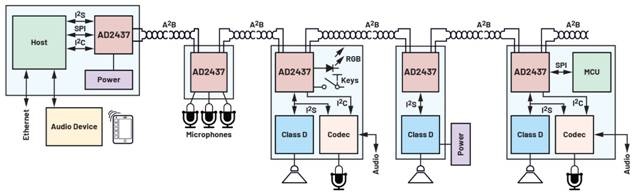
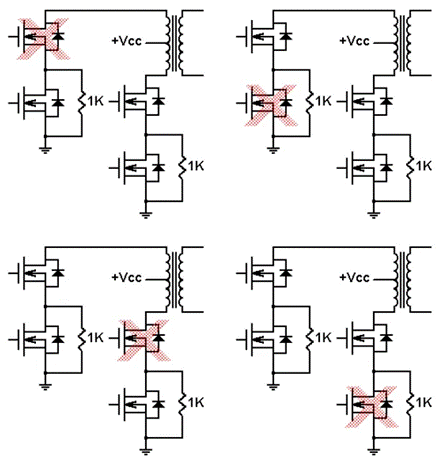
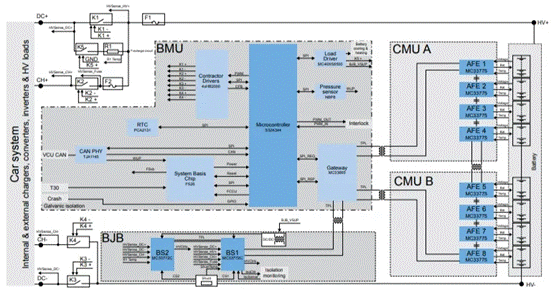
在许多的图画切割算法中，含糊C均值(FCM)切割算法是现在使用最广泛的切割算法之一。最早由Dunn提出，后经Bezdek改进。因为含糊集理论对图画的不确定性有较好的描绘才能，因而FCM算法在医学图画切割中取得了杰出的切割作用。最早把FCM算法用于医学脑部图画切割的是LiC L等人。因为医学图画常有各种不知道噪声，因而给切割带来很大的困难。已有一种改进的FCM(IFCM)算法用来处理该问题，并取得了很好的作用 。在此基础上，本文提出一种新的FCM改进算法，即Sigma-IFCM(Sigma Improved Fuzzy C-Means)算法。这种新算法用Sigma过滤器理论考虑街坊像素，并使用去毛刺和边部润滑技能来批改切割后的脑部图画。从试验成果看，切割作用比 IFCM算法有较大的改进。

1 传统的FCM算法

传统的FCM算法对下列方针函数进行优化：

其间，X={x1，x2，x3，……xn}为数据集；U={uik}为含糊从属度矩阵，uik表明第k个数据归于第i类的从属度；V={vi}为聚类中心调集；||xk-vi||表明xk与vi的间隔，衡量数据点和聚类中心的类似度；m为含糊加权指数且1≤m∞，本文中取m=2；C为聚类的数目且 2≤Cn。

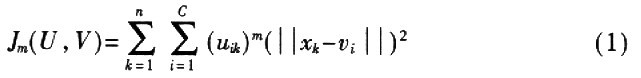
聚类中心核算公式是：

从属度迭代公式是：

2 IFCM算法

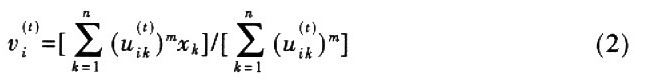
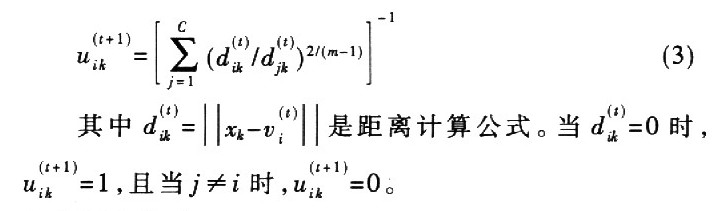
为去除噪声对切割的影响，文献修正了FCM算法的方针函数，但增加了核算复杂度。而文献在每次迭代进程中不只考虑像素点自身的灰度值，还考虑它周边像素点的灰度值，但只修正了d(t)的核算办法，对方针函数的其他部分未作修正。以下为文献的核算公式，皆省掉了上标(t)：

其他核算进程及一些迭代公式与原始FCM算法相同。

3 Sigma-IFCM算法

3．1 Sigma过滤器

在IFCM算法中，考虑街坊点对中心点的影响时，需考虑周边一切的8个街坊点。尽管这样能够去除噪声对切割的影响，但一起对各个聚类的边部也造成了影响，即含糊了聚类的边部。所以在核算某像素点的街坊点时，引证Sigma过滤器(即Edge Preserve过滤器)的理论。首要核算一切街坊点的均值和方差，然后只考虑灰度值在均值的一个邻域内的那些街坊点，这样街坊点数目一般少于8个。
均值μ核算公式为：

其间θ是一个非负的区间调整系数。其他的核算和IFCM算法相同。

3．2 图画的滑润

因为脑部图画的复杂性以及切割算法的原因，切割后的图画总是伴随着毛刺、污点、线划边际凸凹不平等，经过图画的滑润去噪，能够去掉孤立的毛刺、黑斑，滑润边际，添补面状方针内的小孔等，然后进步图画质量。

一般的滑润处理选用n×n的辅佐矩阵(n一般为3~5)作模板，逐行、逐列与图画匹配。当匹配成功时，则把处于模板中心的像素点的切割成果改为与周边像素点的切割成果相同。关于二值图画，依据辅佐矩阵中0、1像元的散布，使处于矩阵中心的像素点从“0”变成“1”，或从“1”变为“0”。

3.2.1 去毛刺

二值图画一般选用图1所示的3×3毛刺去除矩阵，包含其3次90°旋转构成的矩阵。“X”能够为任何值，表明不考虑此处像素点的状况，当矩阵模板在图画上移动时，只需图画与模板匹配，则把模板中心的“1”变为“0”。在算法中，尽管图画不是二值图画，但原理是相同的。即假如模板中心“1”处的像素点切割为一种聚类a，而周边“0”处的像素点切割为另一种聚类b，则把中心像素点变为也归于聚类b，以去除切割后脑部图画边部的毛刺。此刻也不考虑“X”处像素点的切割状况。

3．2．2 线部滑润与孔洞添补

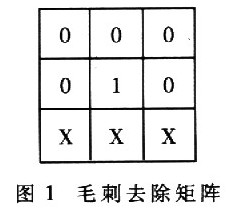
线部滑润和孔洞添补的办法与去毛刺是相同的，仅仅模板不同。一般选用图2所示的3×3线部滑润矩阵，包含其3次90°旋转构成的矩阵。同理．当矩阵模板在图画上移动时，只需图画与模板匹配，则更改模板中心的像素点的切割状况。

3．3 核算过程

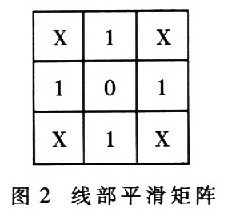
Sigma-IFCM算法方针函数与原始的FCM算法相同，如公式(1)，核算过程如下：

(1)确定聚类数目C，含糊加权指数m以及迭代中止阀值ε；

(2)初始化聚类中心，一般随机发生C个聚类中心；

(3)初始化从属度矩阵U(0)；

(4)使用公式(4)核算d，留意街坊的核算公式是(5)；

(5)使用公式(2)核算各类聚类中心V(t)；

(6)使用公式(3)更新U(t+1)；

(7)挑选便利的矩阵范数来比较U(t)和U(t+1)，假如||U(t+1)-U(t)||≤ε，则中止迭代，不然令t=t+1回来(4)；

(8)对切割后的图画进行去毛刺和边线滑润处理。

最终。每个像素点对各个聚类中心都有一个从属度，把像索点切割到从属度最大的聚类中心即可。

4 试验成果

把原始的IFCM切割算法和改进后的Sigma-IFCM切割算法用于医学图画切割。所挑选的脑部MR模仿图画来自Mcgill大学的MR模仿脑部图画数据库。下载的脑部图画是Tl-weighted的MR图画。本研讨下载了噪声是7％和9％的脑部图画，别离用IFCM算法和SigmaIFCM算法进行切割以及点评比照，成果如表1所示，图中数据均为30幅图画切割成果的平均值。

能够用三个参数来点评切割算法的功能：Under Segmentation(UnS)、Over Segmentation(OvS)和Incorrect SegmentRate(InC)。这三个参数的值越小，阐明算法切割作用越好。一切图画切割成脑白质、脑灰质、脑脊液和布景四部分。公式(4)中的参数λ和ξ别离取值0．47和O．53。公式(5)中的参数θ取1．2。

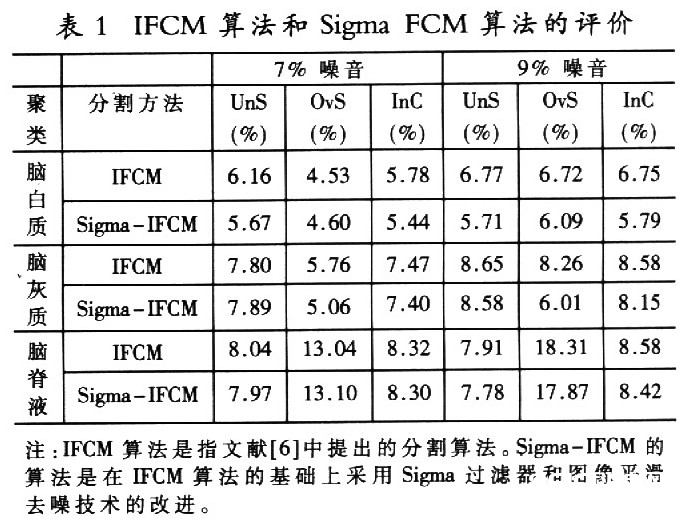
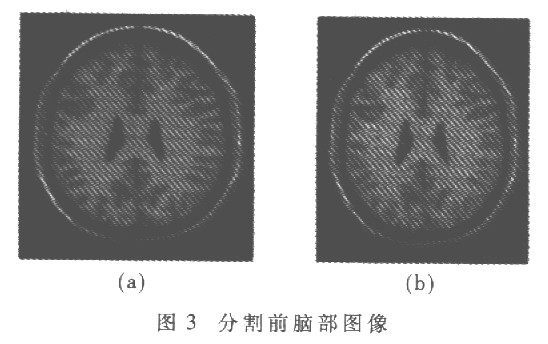
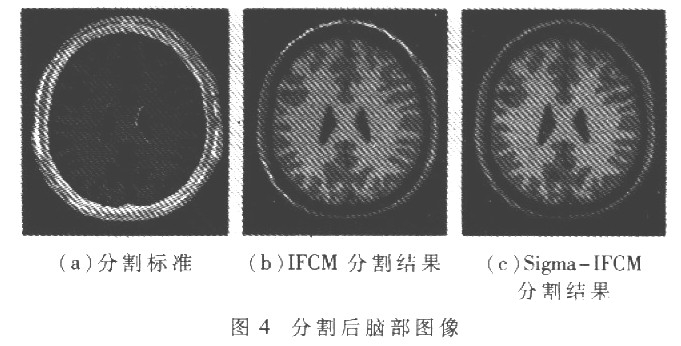
从表1能够看出，关于噪声是9％的脑部图画来说，Sigma-IFCM算法的三个点评参数在不同程度上都比原始IFCM算法的各参数值要小，尤其是脑白质和脑灰质的切割状况更为杰出。这阐明在这种状况下改进后的Sigma-IFCM算法比原始的IFCM算法取得了更好的切割作用。而关于7％噪声的图画， Sigma-IFCM和IFCM算法比较整体切割作用较前者略有优势，但作用不如噪音为9％时显着。从这些数据看，噪声越多的图画，SigmaIFCM算法切割作用越好。图3是切割前的脑部图画，(a)是原始的无噪声模仿MR脑部图画；(b)是具有9％噪声的模仿脑部图画。图4是切割规范和两种算法切割后的脑部图画。

文章提出了一种改进的IFCM脑部MRI图画切割算法。因为医学图画中一般都有各种不知道噪声，选用一般的切割算法会对作用发生很大影响。本文提出的 SigmaIFCM算法改进了像素点街坊的挑选计划，在去除噪声的基础上坚持切割后图画边部的润滑特性，然后引证去毛刺边部润滑的技能来修正切割后的图画。计算成果表明，对图画的切割作用有明显改进。未来的作业能够对初始街坊点的选取进行一些研讨。本文中初始街坊点为周边的8个像素点，能够考虑更大规模如周边的24个街坊点的状况。此外，去毛刺以及边部润滑的办法能够进行进一步的研讨讨论。