除了网上的教程外,还要特别留意,当运算中有浮点的数字时要把,数字后边加上一个f。例如表达式中有4.321参加运算。。当你不在4.321后加f时,stm32F405的片子不知道把他作为单精度float用FPU来运算,,默许可能是作为double来运算(我不确定),运算速度仍是很慢。。牢记一切浮点数字后边加上f,,,,有时分keil会提示warning: #1035-D: single-precision operand implicitly converted to double-precision 这句话的意思便是单精度运算隐式转化成了双精度运算了。这个时分就要在单精度数字后边加个f
keilmdk的设置中完好的define是USE_STDPERIPH_DRIVER,STM32F4XX,__FPU_PRESENT=1,__FPU_USED =1,ARM_MATH_CM4,__CC_ARM
要在MDK中有个选项设置 usr FPU
STM32F4之FPU功用的充分发挥-设置关键
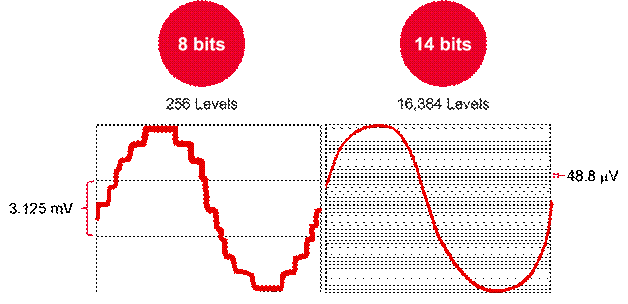
浮点运算一直是定点CPU的难题,比方一个简略的1.1+1.1,定点CPU有必要要依照IEEE-754规范的算法来完结运算,关于8位单片机来说现已完全是噩梦,对32为单片机来说也不会有多大改进。尽管将浮点数进行Q化处理能充分发挥32位单片机的运算功用,可是精度受到限制而不会太高。关于有FPU(浮点运算单元)的单片机或许CPU来说,浮点加法仅仅几条指令的工作。
现在又FPU或许硬件浮点运算才干的主要有高端DSP(比方TI F28335/C6000/DM6XX/OMAP等),通用CPU(X87数学协处理器)和高档的ARM+DSP处理器等。
STM32-F4归于Cortex-M4F构架,这和M0、M3的最大不同便是多了一个F-float,即支撑浮点指令集,因而在处理数学运算时能比M0/M3高出数十倍乃至上百倍的功用,可是要充分发挥FPU的数学功用,还需求一些小小的设置:
1.编译操控选项:尽管STM32F4XX固件库的例程之system_stm32f4XXX.c文件中增加了对应的代码,但给用户评价运用的STM32F4-Discovery例程中却没有,因而MDK4.23编写浮点运算程序时,尽管编译器正确产生了V指令来进行浮点运算,可是由于system_stm32f4XXX.c文件没有启用FPU,因而CPU执行时只认为是遇到不合法指令而跳转到HardFault_Handler()中止中原地踏步。因而要确保这个过错不发生,有必要要在system_init()函数里边增加如下代码:
#if (__FPU_PRESENT == 1) && (__FPU_USED == 1)
SCB-》CPACR |= ((3UL 《《 10*2)|(3UL 《《 11*2));
#endif
由于这个选项是有条件编译操控的,因而需求在工程选项(Project-》OpTIons for target “XXXX”)中的C++/C++选项卡的Define中参加如下的句子:__FPU_PRESENT=1,__FPU_USED =1。这样编译时就参加了发动FPU的代码,CPU也就能正确高效的运用FPU进行简略的加减乘除了。
但这还远远不够。关于杂乱运算,比方三角函数,开方等运算,假如编程时仍是运用math.h头文件,那是无法提高功率的:由于math.h头文件是针对一切ARM处理器的,其运算函数都是依据定点CPU和规范算法(IEEE-754),并没有预见运用FPU的状况,需求许多指令和杂乱的进程才干完结运算,也就增加了运算时刻。因而要充分发挥M4F的浮点功用,就需求运用固件库自带的arm_math.h,这个文件依据编译操控项(__FPU_USED == 1)来决定是运用那一种函数办法:假如没有运用FPU,那就调用keil的规范math.h头文件中界说的函数;假如运用了FPU,那便是用固件库自带的优化函数来解决问题。
在arm_math的最初部分是有这些编译操控信息:
#ifndef _ARM_MATH_H
#define _ARM_MATH_H
#define __CMSIS_GENERIC
#if defined (ARM_MATH_CM4)
#include “core_cm4.h”
#elif defined (ARM_MATH_CM3)
#include “core_cm3.h”
#elif defined (ARM_MATH_CM0)
#include “core_cm0.h”
#else
#include “ARMCM4.h”
#warning “Define either ARM_MATH_CM4 OR ARM_MATH_CM3.。.By Default building on ARM_MATH_CM4.。..。”
#endif
#undef__CMSIS_GENERIC
#include “string.h”
#include “math.h”
便是说假如不运用CMSIS的,就会调用keil自带的规范库函数。不然就用CMSIS的界说。这儿由于是用的STM32F4,所以应该要ARM_MATH_CM4操控,即参加core_cm4.h,不然就用运用ARMCM4.h——但在编译时keil会提示找不到这文件。因而需求在工程选项之C/C++选项卡的define中继续参加句子ARM_MATH_CM4。
参加上述编译操控项之后,高档数学函数的运用根本没问题了,比方正余弦三角函数的核算。但需求留意,假如你直接运用sin()、cos()、sqrt()这样的函数,那成果还算调用keil的math.h,你能够在debug时看对应的代码,其汇编指令为BL.W __hardfp_xxx。因而这时要完结三角函数的核算就要运用arm_sin_f32()或许arm_cos_f32(),用法不变,这两个函数的原型分别在arm_sin_f32.c和arm_cos_f32.c中。经过对256点三角函数表的查询和插值算法得到恣意视点的准确函数值,这就比“原装”的sin()、cos()快多了。
当然有些破例的是开发函数sqrt(),在arm_math.h中是这么界说的:
staTIc __INLINE arm_statusarm_sqrt_f32(float32_t in, float32_t *pOut)
{
if(in 》 0)
{
//#if __FPU_USED
#if (__FPU_USED == 1) && defined ( __CC_ARM)
*pOut = __sqrtf(in);
#else
*pOut = sqrtf(in);
#endif
return (ARM_MATH_SUCCESS);
}
else
{
*pOut = 0.0f;
return (ARM_MATH_ARGUMENT_ERROR);
}
}