1 闻名的Nyquist采样定理
虽然咱们都知道,但仍是提一提。大牛奥本海姆的《信号与体系》中是这样描绘的:
Let x(t) be a band-limited signal with X(jw) = 0 for |w|> wM. Then x(t) is uniquely determined by its samples x(nT),n=1,±1,±2,…,if
ws> 2wMwhere ws= 2 pi/T.
Given these samples, we can reconstruct x(t) by generating a periodic impluse train in which successive impluse have amplitudes that are successive sample values. This impluse train is then processed through an ideal lowpass filter with gain T and cutoff frequency greater than wMand less than ws-wM. The resulting output signal will exactly equal x(t).
来捋一捋,几个点:
带宽有限(band-limited) 采样频率大于2倍信号最高频率后能够无失真的恢复出原始信号
实践中,信号往往是无线带宽的,怎样确保带宽有限?所以,咱们在模仿信号输入端要加一个低通滤波器,使信号变成带宽有限,再运用2.5~3倍的最高信号频率进行采样。关于此咱们下面将模仿数字转化进程将会看到。
虽说是不能小于等于2倍,但选2倍是不是很好呢,理论上,挑选的采样频率越高,越能无失真的恢恢复信号,但采样频率越高,对后端数字体系的处理速度和存储要求也就越高,因而要挑选一个折中的值。
假如后端数字信号处理中的窗口挑选过窄,采样率太高,在一个窗口内很难包容乃至信号的一个周期,这从某方面使得信号无法辨识。比方,数字信号处理的窗口巨细为1024个点,采样率为50KHz,则窗口最多包容1024*(1/50KHz)=20.48ms的信号长度,若信号的一个周期为30ms>20.48ms,这就使得数字信号的处理窗口无法包容一个周期信号,处理的办法便是在满意要求的条件下运用减小采样率或添加窗口长度。
2 模数转化
记住有一次参与中科院核算所的实习书面考试,里边就有这么一道题:模仿信号转化到数字信号要阅历哪两个进程?还好,早有预备,马上填上了采样和量化。咱们下面就来具体剖析下这两个进程,但在剖析之前,咱们先给出一张整个进程的流图,您能够先想想为什么需求各模块。
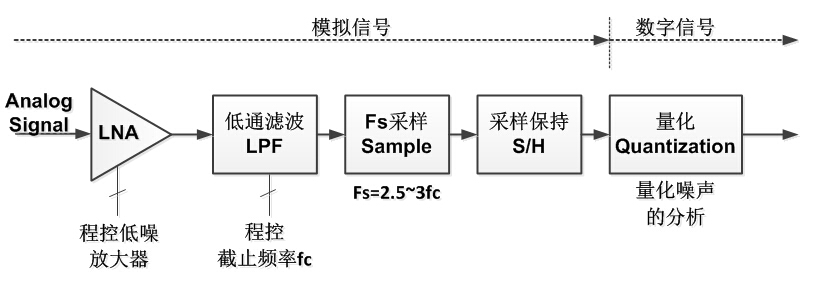
程控扩大器
咱们实践中的模仿信号都是经过传感器收集进来的,做过单片机的人应该熟知DS18B20温度传感器,不好意思,那是数字传感器,也便是说人家做传感器的时分把AD转化也放到传感器里边了。但这并不是遍及的状况,由于温衡量是模仿信号中最简单丈量的量了,而大多数的传感器并没有集成AD转化进程,如大多数的加速度传感器、轰动传感器、声响传感器、电子罗盘,乃至有的GPS(别懵了,GPS也算是一种传感器哦)等,都是模仿输出的。并且由于物理制造的原因,传感器回来的电信号十分细小,一般在几mV(假如是电流,也一般在几mA),这么弱小的信号,假如经过导线或电缆传输很简单就湮灭在噪声中。因而,咱们常常见到模仿传感器的输出线都会运用套上一层塑胶的线,叫屏蔽线(如图)。

屏蔽线只能确保在信号传输到体系之前遭到的搅扰最小,但信号仍要经过处理才干为数字体系运用。在模仿信号(尤其是高频信号)的输入端首先要运用低噪声扩大器对信号进行扩大,这个扩大器有特别的要求,必定是低噪声,咱们现已知道,模仿信号信号现已十分弱小,假如扩大器还存在必定的噪声,在噪声叠加之后扩大出来的信号或许现已不再是原信号了。已然提到低噪声,那么低噪声是怎样衡量的呢?这能够经过扩大器噪声系数(NF)来定,
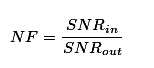
噪声系数界说为扩大器输入信号与输出信号的信噪比。其物理意义是:信号经过扩大器之后,由于扩大器发生噪声,使信噪比变坏;信噪比下降的倍数便是噪声系数。噪声系数通常用dB表明,
实践中除了考虑低噪声系数外,还要考虑扩大器的带宽和频率规模以及最重要的扩大增益。由于输入信号的强度或许时变,选用程序可控(程控)的扩大增益确保信号能到达满度而又不会呈现饱满(实践中要做到这一点仍是很难的)。
低通滤波器
在Nyquist采样定理中现已提过,要满意采样定理有必要要求信号带宽有限,运用大于2倍的最高信号频率采样才干确保信号的不混叠。低通滤波器的一个考虑便是使信号带宽有限,以便于后期的信号采样,这个低通滤波器是硬件完成的。另一方面,实践状况中咱们也只会对某个频频段的信号感兴趣,低通滤波器的另一个考虑便是滤波得到感兴趣的信号。比方,丈量轿车声响信号,其频率大部分在5KHz以下,咱们则能够设置低通滤波器的截止频率在7KHz左右。
程控的完成办法便是运用模仿通道挑选芯片(如74VHC4051等)。
NOTES:
有关滤波与程控的电路规划请参阅文献[1].
在采样之前的一切电路完成计划叫信号调度电路。这样,咱们就能够依据这个词处处Google/Baidu文献了。
采样及采样坚持
采样形似有一套完好的理论,便是《数字信号处理》书中的一堆公式推导,咱们这儿当然不会那么去说。其实采样最中心的问题便是采样率挑选的问题。
依据实践,挑选频率分辨率df 挑选做DFT得点数N,由于DFT时域点数和改换后频域点数相同,则采样率可确认,Fs=N*df Fs是否满意Nyquist的采样定理?是,OK,不然添加点数N,从头核算2。
咱们期望df越小越好,但实践上,df越小,N越大,核算量和存储量随之增大。一般取N为为2的整数次幂,缺乏则在尾端补0。
这儿给出我的一个挑选Fs的计划流程图,仅供参阅。
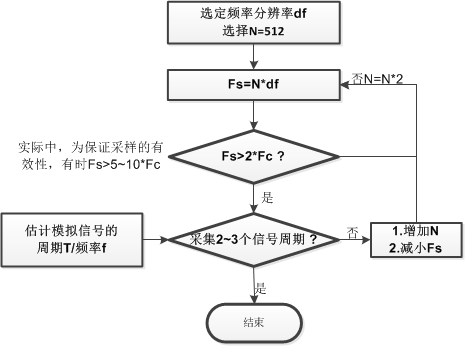
采样后还有一个重要的操作是采样坚持(S/H)操作,采样脉冲采样后无法马上量化,这个进程要等候很短的一个时刻,硬件上一般0.几个us,等候量化器的量化。
留意,在量化之前,一切的信号都是模仿信号,模仿信号就有许多搅扰的问题需求考虑,这儿仅仅从总体上给出我对整个进程的了解。更多细化的计划还需求依据实践信号进行研究。
量化
咱们能够先直观的看一下量化的进程,

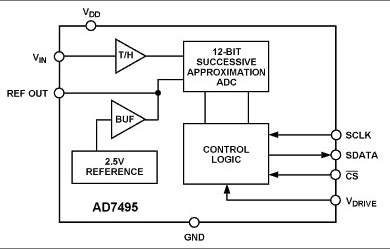
量化有个要害的参数,叫量化位数,在一切的AD转化芯片(如AD7606)上都能看到这个要害的参数,常见的有8bit,10bit,12bits,16bit和24bit。
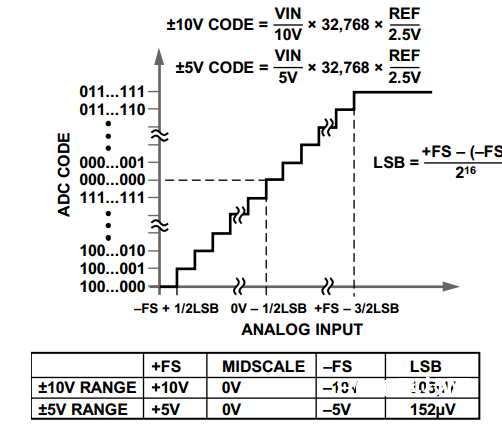
如上图,以AD7606为例,AD7606是16bit的AD芯片,量化位数指用16bit来表明接连信号的幅值。因而,考虑AD的丈量规模(AD7606有两种:±5V和±10V),则AD分辨率是
±5V: (5V-(-5V)) / (2^16) = 152 uV
±10V: (10V-(-10V)) / (2^16) = 305 uV
量化位数越高,AD分辨率越高,习惯上,AD分辨率用常用LSB标明。
因而,AD7606中关于某个输入模仿电压值,由于存在正负电压,若以0V为中心电压值,规模为±5V时AD转化电压可核算为
AD7606若运用内部参阅电压,Vref=2.5V。哦对了,这又呈现个参阅电压。参阅电压与AD量化的完成方法有关,赶快度上分串行和并行,串行包含逐次迫临型,并行方法包含并行比较式,如下图(左:串行,右:并行)。AD7606是运用逐次迫临型的方法。
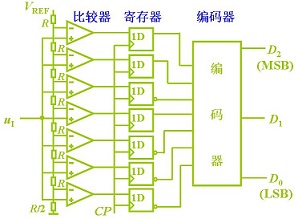
AD转化芯片别的两个重要参数是转化时刻(转化速率)。并行AD的转化速率比串行的要高。但并行比较的方法中电阻的精度对量化有影响。
接着,咱们还将介绍一个重要的概念:量化噪声。量化噪声对应量化信噪比,
SNRq= (6.02N + 4.77) dB
其间N为量化位数,且不去管这个公式是怎样得到的(具体推导可参阅文献[2]),关于
N=12, SNRq≈ 70dB
N=16, SNRq≈ 94dB
从中能够看出:每添加1bit量化位数,SNRq将进步6.02dB,在规划进程中,假如对方有信噪比的要求,则在ADC选型时就要挑选适宜位数的ADC芯片。
显着的,并不是量化位数越高越好,量化位数的进步将对本钱、转化速度、存储空间与数据吞吐量等很多方面提出更高的要求。一起,咱们尽量进步量化噪声的条件是信号的SNR现已比较低了,假如信号的SNR比量化噪声还高,努力进步量化噪声将是舍本求末的做法。