最优化理率与算法是一个重要的数学分支,它所研讨的问题是,在很多的计划中什么样的计划最优以及怎样找出最优计划。早在公元前500年,古希腊数学家毕达哥拉斯就已发现了黄金分割法,17世纪牛顿创造微积分时现已提出极值问题,后来又呈现拉格朗日乘数法;1847年柯西提出了最速下降法,还有求无约束极值的变分法,这些统称为古典最优化办法。
因为出产和科学研讨迅猛发展,许多最优化问题已无法用古典办法处理,又因为电子核算机日益遍及,使最优化问题的研讨不只成为一种迫切需要,并且有了求解的有力东西。现在现已有许多核算机算法处理最优化问题,如Kuhn-Tucker 定理、Be11man 最优化原理和动态规划、pONTRIAGIN 的极大值原理以及Ka1man 的关于随机控制系统最优滤波器。
最优化节点坐落函数选板的“数学→最优化”,如图所示。
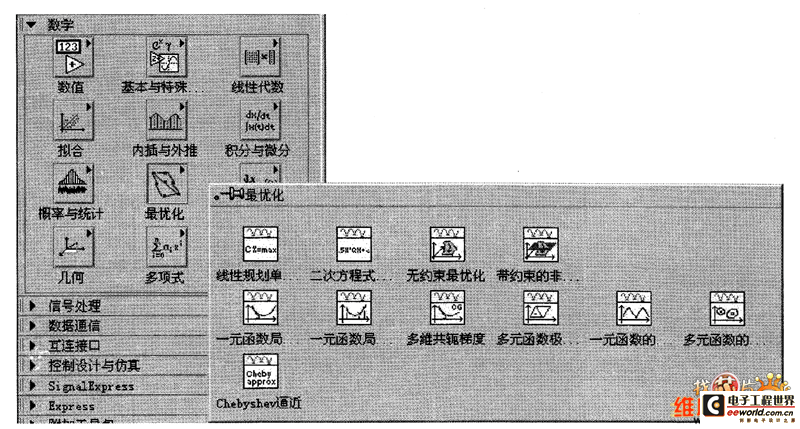
如图 最优化子选板
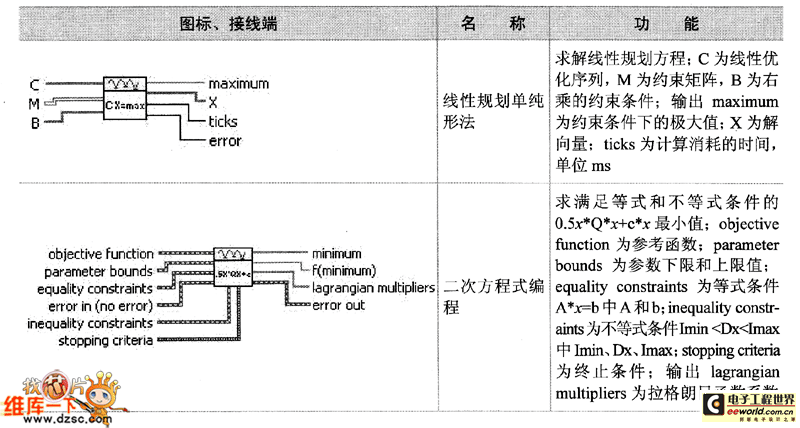
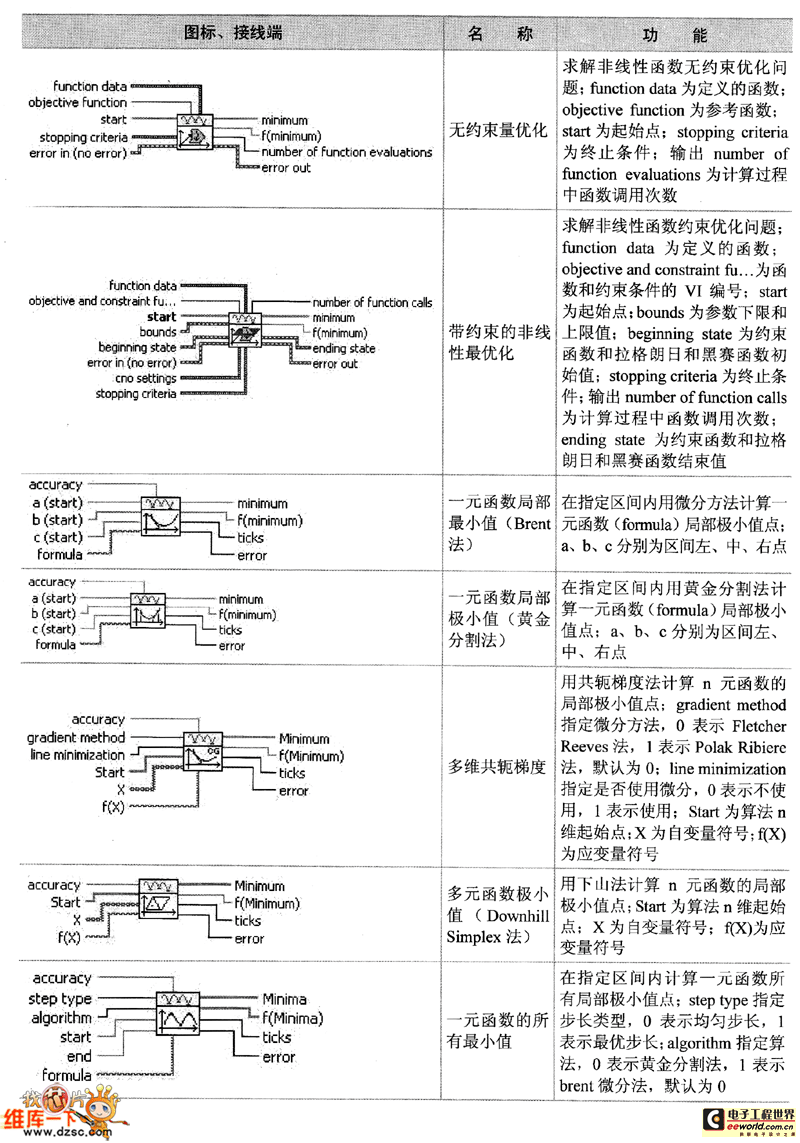
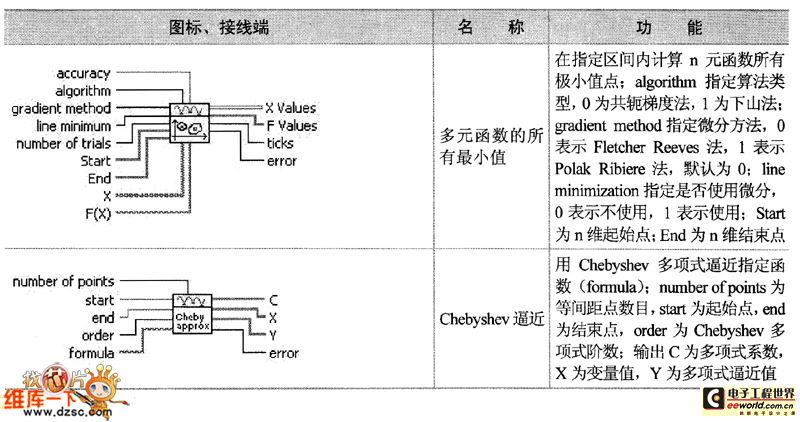
如表具体列出了最优化子选板中函数和Ⅵ节点的图标、接线端、图标和功用。其间常见参数阐明如下。
accuaracy:指定核算的精度,默以为1e-8。
mlnlmum:极小值对应的自变量值。
f(minimum):函数极小值。
如表 最优化子选板节点