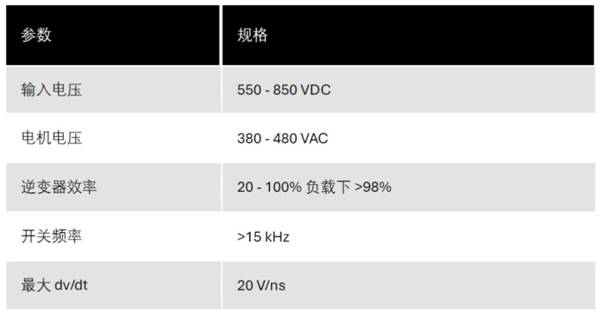
- A* 查找算法——图形查找算法,从给定起点到给定结尾核算出途径。其间运用了一种启发式的预算,为每个节点预算经过该节点的最佳途径,并以之为各个地址排定次第。算法以得到的次第拜访这些节点。因而,A*查找算法是最佳优先查找的典范。
- 集束查找(又叫定向查找,Beam Search)——最佳优先查找算法的优化。运用启发式函数评价它查看的每个节点的才能。不过,集束查找只能在每个深度中发现最前面的m个最契合条件的节点,m是固定数字——集束的宽度。
- 二分查找(Binary Search)——在线性数组中找特定值的算法,每个进程去掉一半不契合要求的数据。
- 分支界定算法(Branch and Bound)——在多种最优化问题中寻觅特定最优化处理方案的算法,特别是针对离散、组合的最优化。
- Buchberger算法——一种数学算法,可将其视为针对单变量最大公约数求解的欧几里得算法和线性体系中高斯消元法的泛化。
- 数据压缩——采用特定编码方案,运用更少的字节数(或是其他信息承载单元)对信息编码的进程,又叫来历编码。
- Diffie-Hellman密钥交流算法——一种加密协议,答应两边在事前不了解对方的状况下,在不安全的通讯信道中,一同树立同享密钥。该密钥今后可与一个对称暗码一同,加密后续通讯。
- Dijkstra算法——针对没有负值权重边的有向图,核算其间的单一同点最短算法。
- 离散微分算法(Discrete differentiation)
- 动态规划算法(Dynamic Programming)——展现相互掩盖的子问题和最优子架构算法
- 欧几里得算法(Euclidean algorithm)——核算两个整数的最大公约数。最陈旧的算法之一,出现在公元前300前欧几里得的《几许本来》。
- 希望-最大算法(Expectation-maximization algorithm,又叫EM-Training)——在核算核算中,希望-最大算法在概率模型中寻觅或许性最大的参数预算值,其间模型依赖于未发现的潜在变量。EM在两个进程中替换核算,第一步是核算希望,运用对躲藏变量的现有估计值,核算其最大或许估计值;第二步是最大化,最大化在第一步上求得的最大或许值来核算参数的值。
- 快速傅里叶变换(Fast Fourier transform,FFT)——核算离散的傅里叶变换(DFT)及其回转。该算法运用规模很广,从数字信号处理到处理偏微分方程,到快速核算大整数乘积。
- 梯度下降(Gradient descent)——一种数学上的最优化算法。
- 哈希算法(Hashing)
- 堆排序(Heaps)
- Karatsuba乘法——需求完结上千位整数的乘法的体系中运用,比方核算机代数体系和大数程序库,假如运用长乘法,速度太慢。该算法发现于1962年。
- LLL 算法(Lenstra-Lenstra-Lovaszlattice reduction)——以格规约(lattice)基数为输入,输出短正交向量基数。LLL算法在以下公共密钥加密办法中有许多运用:背包加密体系(knapsack)、有特定设置的RSA加密等等。
- 最大流量算法(Maximum flow)——该算法企图从一个流量网络中找到最大的流。它优势被界说为找到这样一个流的值。最大流问题能够看作更杂乱的网络流问题的特定状况。最大流与网络中的界面有关,这便是最大流-最小截定理(Max-flow min-cut theorem)。Ford-Fulkerson 能找到一个流网络中的最大流。
- 兼并排序(Merge Sort)
- 牛顿法(Newtons method)——求非线性方程(组)零点的一种重要的迭代法。
- Q- learning学习算法——这是一种经过学习动作值函数(action-value function)完结的强化学习算法,函数采用在给定状况的给定动作,并核算出希望的功效价值,在尔后遵从固定的战略。Q-leanring的优势是,在不需求环境模型的状况下,能够比照可采用举动的希望功效。
- 两次筛法(Quadratic Sieve)——现代整数因子分化算法,在实践中,是现在已知第二快的此类算法(仅次于数域筛法Number Field Sieve)。关于110位以下的十位整数,它仍是最快的,并且都以为它比数域筛法更简略。
- RANSAC——是“RANdom SAmple Consensus”的缩写。该算法依据一系列调查得到的数据,数据中包含异常值,预算一个数学模型的参数值。其根本假设是:数据包含非异化值,也便是能够经过某些模型参数解说的值,异化值便是那些不契合模型的数据点。
- RSA——公钥加密算法。首个适用于以签名作为加密的算法。RSA在电商职业中仍大规模运用,我们也信任它有满足安全长度的公钥。
- Schönhage-Strassen算法——在数学中,Schönhage-Strassen算法是用来完结大整数的乘法的快速渐近算法。其算法杂乱度为:O(N log(N) log(log(N))),该算法运用了傅里叶变换。
- 单纯型算法(Simplex Algorithm)——在数学的优化理论中,单纯型算法是常用的技能,用来找到线性规划问题的数值解。线性规划问题包含在一组实变量上的一系列线性不等式组,以及一个等候最大化(或最小化)的固定线性函数。
- 奇异值分化(Singular value decomposition,简称SVD)——在线性代数中,SVD是重要的实数或复数矩阵的分化办法,在信号处理和核算中有多种运用,比方核算矩阵的伪逆矩阵(以求解最小二乘法问题)、处理超定线性体系(overdeterminedlinear systems)、矩阵迫临、数值天气预报等等。
- 求解线性方程组(Solving a system of linear equations)——线性方程组是数学中最陈旧的问题,它们有许多运用,比方在数字信号处理、线性规划中的预算和猜测、数值剖析中的非线性问题迫临等等。求解线性方程组,能够运用高斯—约当消去法(Gauss-Jordan elimination),或是柯列斯基分化(Cholesky decomposition)。
- Strukturtensor算法——运用于模式识别范畴,为一切像素找出一种核算办法,看看该像素是否处于同质区域(homogenous region),看看它是否归于边际,仍是是一个极点。
- 兼并查找算法(Union-find)——给定一组元素,该算法常常用来把这些元素分为多个别离的、互相不重合的组。不相交集(disjoint-set)的数据结构能够盯梢这样的切分办法。兼并查找算法能够在此种数据结构上完结两个有用的操作:
- 查找:判别某特定元素归于哪个组。
- 兼并:联合或兼并两个组为一个组。
- 维特比算法(Viterbi algorithm)——寻觅躲藏状况最有或许序列的动态规划算法,这种序列被称为维特比途径,其结果是一系列能够调查到的事情,特别是在躲藏的Markov模型中。
32个算法介绍
A*搜索算法——图形搜索算法,从给定起点到给定终点计算出路径。其中使用了一种启发式的估算,为每个节点估算通过该节点的最佳路径,并以
声明:本文内容来自网络转载或用户投稿,文章版权归原作者和原出处所有。文中观点,不代表本站立场。若有侵权请联系本站删除(kf@86ic.com)https://www.86ic.net/ziliao/318679.html