学习傅里叶变换需求面临很多的数学公式,数学功底较差的同学听到傅里叶变换就头疼。事实上,许多数学功底好的数字信号处理专业的同学也不用定了解傅里叶变换的实在含义,不能做到学以致用!
事实上,傅里叶变换的相关运算现已十分老练,有现成函数能够调用。关于绝大部分只需用好傅里叶变换的同学,重要的不是去记那些单调的公式,而是解傅里叶变换的含义及含义。
本文企图不用一个数学公式,选用较为浅显的言语浅显易懂的论述傅里叶变换的含义、含义及办法,期望咱们能够愈加接近傅里叶变换,用好傅里叶变换。
一巨大的傅里叶、巨大的争议!
1807年,39岁的法国数学家傅里叶于法国科学学会上展现了一篇论文(此刻不能算宣布,该论文要到21年之后宣布),论文中有个在其时极具争议的结论:“任何接连周期信号能够由一组恰当的正弦曲线组合而成”。
这篇论文,引起了法国别的两位闻名数学家拉普拉斯和拉格朗日的极度重视!

58岁的拉普拉斯拥护傅里叶的观念。
71岁的拉格朗日(形似现在的院士,不用退休)则对立,对立的理由是“正弦曲线无法组合成一个带有棱角的信号” 。屈服于朗格朗日的声威,该论文直到朗格朗日逝世后的第15年才得以宣布。
之后的科学家证明:傅里叶和拉格朗日都是对的!
有限数量的正弦曲线确实无法组合成一个带有棱角的信号,但是,无限数量的正弦曲线的组合从能量的视点能够十分无限迫临带有棱角的信号。
二傅里叶变换的界说
后人将傅里叶的结论进行了扩展:满意必定条件的函数能够表明成三角函数(正弦和/或余弦函数)或许它们的积分的线性组合。怎么得到这个线性组合呢?这就需求傅里叶变换。
必定条件是什么呢?
这是数学家研讨的问题,关于大多数搞电参量丈量的工程师而言,不用重视这个问题,由于,电参量丈量中遇到的周期信号,都满意这个条件。
这样,在电参量丈量剖析中,咱们能够用更浅显的话来描绘傅里叶变换:
恣意周期信号能够分化为直流重量和一组不同幅值、频率、相位的正弦波。分化的办法便是傅里叶变换。
而且,这些正弦波的频率契合一个规矩:是某个频率的整数倍。这个频率,就称为基波频率,而其它频率称为谐波频率。假如谐波的频率是基波频率的N倍,就称为N次谐波。直流重量的频率为零,是基波频率的零倍,也可称零次谐波。
三傅里叶变换的含义
1为什么要进行傅里叶变换呢?
傅里叶变换是描绘信号的需求。
只要能反映信号的特征,描绘办法越简略越好!
信号特征能够用特征值进行量化。
所谓特征值,是指能够定量描绘一个波形的某种特征的数值。全面描绘一个波形,或许需求多个特征值。
比如说:正弦波能够用幅值和频率两个特征值全面描绘;方波能够用幅值、频率和占空比三个特征值全面描绘(单个周期信号不考虑相位)。
上述特征值,咱们能够经过示波器观测实时波形获取,称为时域剖析法。事实上,许多人都习惯于时域剖析法,想要了解一个信号时,必定会说:“让我看看波形!”
但是,除了一些常见的规矩信号,许多时分,给你波形看,你也看不理解!
杂乱的不讲,看看下面这个波形,能看出道道吗?
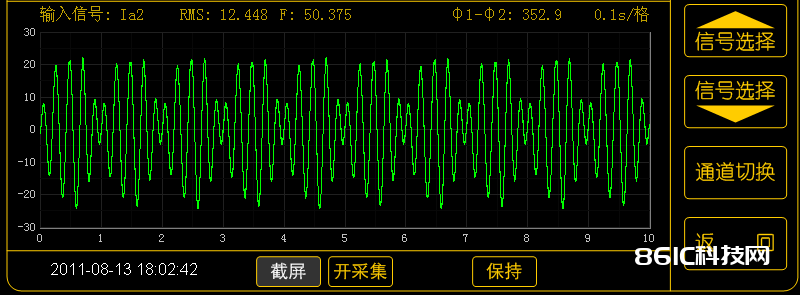
咱们能看到的仅仅是一个相似正弦波的波形,其幅值在依照必定的规矩改变。
怎么记载这个波形的信息呢?尤其是量化的记载!
很难!
事实上,上述波形选用傅里叶变换后,便是一个50Hz的正弦波上叠加一个40Hz的正弦波,两者起伏不同,40Hz的起伏越大,动摇起伏就越大,而动摇的频率便是两者的差频10Hz(三相异步电动机叠频温升实验时的电流波形)。









