MATLAB中进行软件滤波仿真
我身边有些朋友说现在在校园学习什么拉氏改换,Z改换,傅立叶改换没有用,传递函数没有用,差分方程没有用,仅仅坐而论道,我这儿先就传递函数和拉氏改换和差分方程介绍几点自不量力的观点,咱们学习拉氏改换首要是为了从脱离时域,由于时域剖析有它的难度指数,咱们从时域映射到S域,意图只要一个,那便是简化核算,正如咱们在时域要核算卷积过来,卷积曩昔,咱们把它映射到S域往后,便是乘积过来积乘曩昔,相对来说,乘积要比卷积的积分要温顺的多,然后咱们在S域里边得到定论往后,再将其反映射回到时域,然后自然地在时域运用其所得的定论了。
以下仅举两个比如,就一阶惯性惯性滤波器和二阶滤波器的算法完成做扼要介绍,如下,咱们很简略写出其传递函数,G(s)=…/…,在G(s)中,S项即为微分项,核算机中,微分即为差分,由于咱们是因果体系,即运用后项差分替代微分,例如:sU(t)转化为U(K)-U(K-1),如此一来,代入传递函数简将传递函数化后,再将其写编成软件仿真。相对于我自己,觉得最快的方法便是MATLAB算法仿真,如下即为仿真成果,二阶滤波器仿真同理。在调整相应参数的时分,即可当作在硬件电路中调整R、C的参数相同。
一、一阶惯性滤波器软件完成

clear,clc
Data = load(‘usefuldata.txt’);
plot( Data );
title(‘original data’);
T = 5;%电路归纳参数(交融了电容电阻和微分时刻参数)
Data2 = zeros( size( Data ) );
Data2( 1 ) = Data( 1 );
[ H V ] = size( Data );
for i =2:V
Data2( i ) = ( Data( i ) + T * Data2( i – 1) ) / ( T+1 );
end
figure
plot(Data2);
title(‘handled data’);
以下是仿真成果:
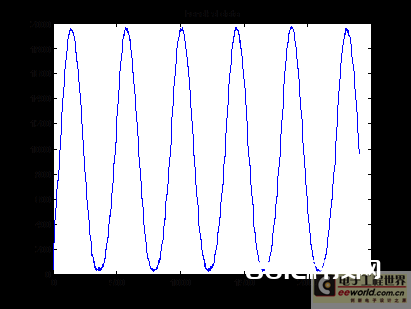
1、原始数据的波形:

2、滤波往后的数据的波形:
二、二阶惯性滤波器软件完成
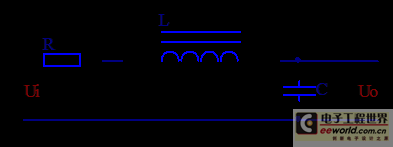
MATLAB代码如下:
%LRC滤波器软件完成
clear,clc
Data = load(‘usefuldata.txt’);
plot( Data );
title(‘original data’);
T = 0.001;%微分时刻
R = 100000;%电路电阻
C = 0.1;%滤波%&&&&&%
L = 0.02;%滤波电感
Data2 = zeros( size( Data ) );
Data2( 1 ) = Data( 1 );
Data2( 2 ) = Data( 2 );
[ H V ] = size( Data );
for i =3:V
Data2( i ) = ( Data( i ) + ( T * R * C + 2 * T * L * C )… %标明本行还没有完毕
* Data2( i – 1) – T * L * C * Data2( i – 2 ) ) / ( T * L * C + 1 + T * R * C );
end
figure
plot(Data2);
title(‘handled data’);
以下是仿真成果:
1、原始数据的波形:

2、滤波往后的数据的波形:
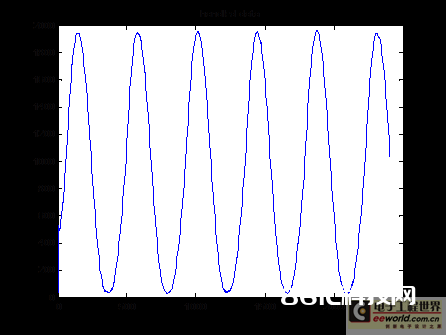
以上程序中,仅仅用了MATLAB的仿真功用,没有调用MATLAB的滤波函数,所以完全可以将MATLAB程序翻译成C言语后嵌入下位机软件中运用。
尽管上述两类滤波算法并没有FFT和小波剖析进行滤波来的巨大上,更没有后两者来的直接,但在一些简略数据处理中有它共同的优势。主张AD采样进来的数据进行简略滤波,由于一般使用都不会在AD上面做很准确的基准电压。









