文章转自ADI官网,版权归属原作者一切
一切DAC都会表现出必定程度的谐波失真,谐波失真是用来衡量当DAC输入端选用一个抱负的均匀采样正弦波的数值序列驱动时,其输出端能在多大程度上再现这个抱负的正弦波。因为DAC的瞬态和静态特性并不抱负,因而输出频谱将会包括谐波成分。DAC的瞬态输出特性包括压摆率约束、非对称上升和下降时刻、有限树立时刻。静态特性与传递函数违背直线的程度有关。本文将要点评论静态特性,并论述一种由输出频谱中观察到的谐波成分导出DAC传递函数的办法。剖析中假定,传递函数而非瞬态输出特性是所观察到的谐波失真的首要来历。此假定在低频时建立。
DAC传递函数
图1显现一个抱负的DAC传递函数,它是一条斜线,y=mx+b. 数字输入坐落x轴,模仿输出坐落y轴。
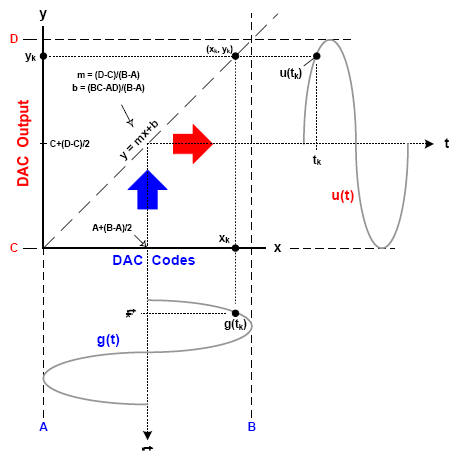
x轴上的方针规模是从左面的最小码(A)到右边的最大码(B)。y轴上的方针规模是从底部的最小输出值(C)到挨近顶部的最大输出值(D)。界说抱负传递函数的斜率(m)和y轴截距(b)的方程式用鸿沟值A、B、C、D表明。信号g(t)代表一个无失真的正弦波,由A至B规模内的数字输入组成,时刻轴向下。信号u(t)代表模仿输出,其值在C至D规模内,时刻轴向右。
输出信号是经过传递函数反射的输入信号。请留意,输出信号是将g(t)上各点链接到u(t)上相应点的成果。图1显现在特定时刻点 t=tk的传递操作比如,该时 间 点 确认输入信号上的点g(tk)。传递函数进而将g(tk)链接到输出信号上的相应点u(tk)。关于抱负的线性传递函数,u(t)与g(t)成份额联系。请留意,g(tk)对应于x轴上的点xk,它经过传递函数反射至y轴上的点yk。凭借关于耦合点集(g(tn),u(tn))的已有常识,能够确认传递函数上的相关点(x n,y n)。因而,经过输入信号g(t)上的点与输出信号u(t)上的点之间的联系,彻底可界说传递函数。
关于N位DAC,鸿沟值A和B取特定值,即 A = 0 且 B = 2N–1。 而为了便利起见,指定鸿沟值C和D为 C = A 且 D = B。 这样意味实践DAC输出信号的份额和偏移,因而其峰峰值规模为0至 2N–1。 运用A、B、C、D的这些值,因为斜率 m = 1 且截距 b = 0。所以抱负传递函数可简化为y=x。
到目前为止,评论的要点仍是抱负的DAC传递函数,但现在咱们有了能够处理失真DAC传递函数f(x)的东西,如图2所示。需求留意的首要特点是:传递函数不再是直线y=x,而是一个形状函数f(x);图中随意以滑润弧形来表明。f(x)对输出函数u(t)的影响也相同重要。抱负输入g(t)经过传递函数f(x)反射,发生失真输出u(t)。与现成DAC的传递函数比较,图中所示的弧形传递函数较为夸大,仅为加强阐明效果罢了。现代DAC的传递函数与抱负的直线几乎没有差错,但即便最细小的差错也会导致输出频谱中呈现谐波杂散。
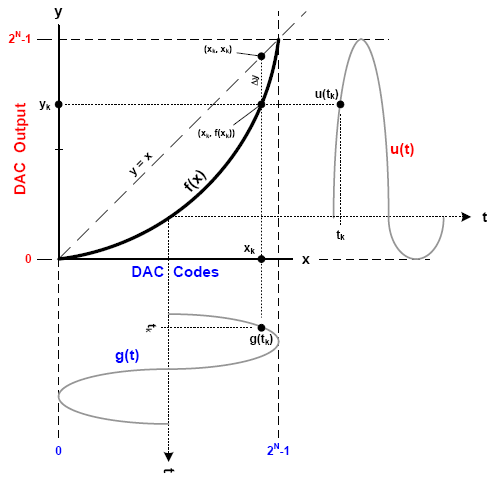
能否成功重构DAC传递函数,取决于是否能经过已知的g(t)和u(t)确认各点(xk,f(xk))。这一进程分为两步:首要选用一个代表抱负采样正弦波的数值序列驱动DAC输入,运用频谱剖析仪丈量DAC输出,并记载基波信号和尽或许多谐波成分的幅值;然后将测得的谐波幅值转化为特定形状的传递函数。假如操作妥当,将g(t)代入f(x)仿真u(t)将发生与丈量成果相同的谐波失真值。
第一步:丈量DAC谐波
第一步需求一个输入序列,用来代表一个以等距时刻距离采样的抱负正弦波周期。方针是重构DAC传递函数,因而从0到2N–1的每个DAC码有必要在输入信号中至少呈现一次。输入序列需求2N以上的采样点才干以等距距离运用每个DAC码,实践上至少需求2N+3个采样才干保证每个码都呈现。下式可发生2K DAC码的抱负正弦序列(K≥N+3)。函数round{x}将x舍入为最近的整数。
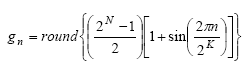 |
where n=0,1,2,3, … 2K–1 |
此方程式假定DAC将规范二进制格局的数字输入字解码为0至2N–1规模内的无符号整数。关于偏移二进制或二进制补码DAC,有必要调整gn以表明负值。
数值序列(gn)以采样速率f s重复供给给DAC,因而DAC输出频谱含有频率f0=f s/2k的基波信号。谐波呈现在2f0、3f0、4f0和f0的其它整数倍。因为DAC输出频谱具有采样性质,因而这些谐波的起伏受sin(x)/x呼应的约束。不过,f0与fs比较微乎其微,因而sin(x)/x呼应实践上是平整的,可忽略不计。例如,关于一个8位DAC,K≥11且f0≤fs/2048,100次谐波的sin(x)/x将不超越0.39%(0.034 dB)。
为了精确重构传递函数f(x),需求依据谐波数(h)集尽或许记载更多谐波的幅值。这些整数从h=1(基波频率)至h=H,其间H表明取丈量幅值的最高谐波数。例如,关于10次谐波的丈量,H=10,该谐波数集为h={1, 2, 3, .. 10}。
然后,将各丈量谐波的幅值(M)与其谐波数相关。例如,M1是1次谐波(基波)的幅值,M2是2次谐波的幅值,依此类推至MH。谐波幅值通常用相关于基波幅值的分贝数(dBc)来衡量。dBc转化为线性单位的公式如下:
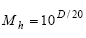
其间D表明测得的谐波幅值,单位为dBc。例如,假如3次谐波的幅值为–40 dBc,则线性幅值M3=10–40/20或0.01。M1一直等于1,因为依据界说,基波的幅值为0 dBc。
第二步:重构DAC传递函数
该进程的第二步涉及到将谐波丈量成果与传递函数相关。f(x)上的点取决于g(t)和u(t)上对应点之间的联系,因而首要有必要将频域中的谐波幅值转化到时域。请留意,组成g(t)的DAC码与g(t)正弦方式的相关时刻点一一对应。因而,构成g(t)的DAC码与时域相关。此外,u(t)经过f(x)与g(t)相关,而g(t)是一个时域函数,因而u(t)也有必要表明为时域函数。这样就能将g(t)中的各时刻点tk链接到u(t)中的相关时刻点,然后由g(t)和u(t)确认f(x)。
将谐波幅值转化到时域十分困难,因为f(x)有必要清晰与g(t)中的各或许DAC码(0至2N–1)相关。g(t)是一个抱负正弦波,因而保证仅有性的仅有办法是将规模约束在该正弦波单调添加的方位,如图3加粗部分所示。假如没有这一约束条件,f(x)上的一个点或许会映射到g(t)上的两个点,然后导致不清晰。
为演示这种不定性,请幻想将区间T向下移动。现在,f(x)上的点(xk,f(xk))能够与g(t)上的两个点相关,这是不行承受的。将规模T约束在图中所示方位,将不存在不定性。g(t)为正弦波,因而所需规模T对应于½周期,其初始相位偏移为3π/2弧度。
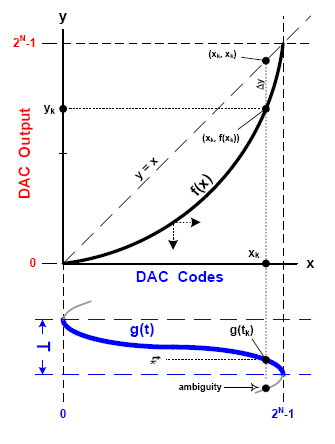
g(t)的规模受T约束意味着u(t)也具有相似的规模约束。因而,将所记载的谐波幅值转化到时域时,有必要保证将u(t)约束在与g(t)相同的规模T,如图4所示。
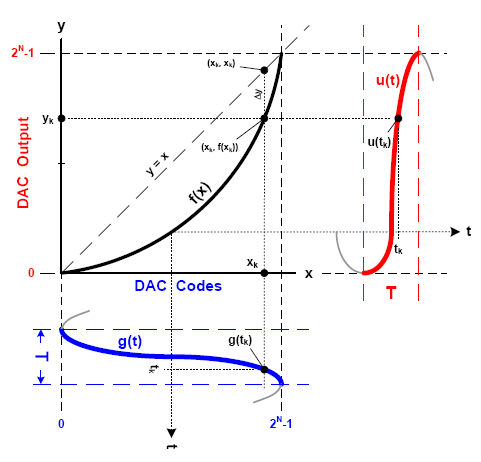
请留意,实践的时刻规模T无关紧要,因为f(x)仅在g(t)和u(t)二者的幅值之间起转化效果。为简化剖析,将基波频率(f0)归一化为1。因而,2次谐波的频率为2,3次谐波的频率为3,如此类推。所以,谐波频率与谐波数(h)持平:fh=h。这一快捷联系可简化从谐波丈量成果Mh创立u(t)的数学核算。
正弦波的一般时域表达式为:
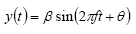 |
其间β为峰值振幅,θ为初始相位偏移。 |
用h替代f,并用Mh替代β,能够获得各谐波uh(t)的时域表达式。不过应记住,g(t)偏 移3π/2弧度。此外,g(t)与u(t)之间经过f(x)相关意味着g(t)和u(t)在相位上是对准的。用3π/2替代θ可供给所需的对准。下式中,请留意0≤t<1且π替代了2π,意图是将基波约束在规模T所表明的半个周期:
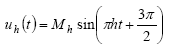
运用各谐波uh(t)的时域表达式,便能够重构复合输出u(t),表明为基波和谐波信号的和:
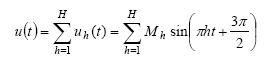
如前所述,咱们的方针是将g(t)与u(t)相关以重构DAC传递函数f(x)。此外,g(t)有必要刚好由2N个样本组成,以便与f(x)上的点一一对应。因而,g(t)的样本核算公式为:
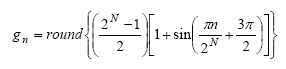 |
(n=0,1,2,3 .. 2N–1) |
g(t)由2N个样本组成,因而由包括2N个采样的u(t)采样值集重构f(x)似乎是合理的。但是,现实却是至少需求2N+3个采样才干为较小的Mh值供给恰当的精度。这种情况下,u(t)各采样点的核算公式应如下:
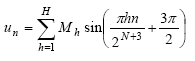 |
(n=0,1,2,3 .. 2N+3–1) |
请留意,这将导致u(t)所含的采样数多于g(t),u(t)的多个样本或许与f(x)和g(t)上的一个点对应,然后使u(t)和g(t)到f(x)的映射联系复杂化。因而,有必要对特定的样本组求平均值,以便供给到f(x)的合理映射。下面的伪代码反映了所需的映射联系,其间假定运用一个N位DAC,g(t)有2N个点,u(t)有2N+3个点。阵列DacXfr含有2N个元素,初始值均为0。履行该代码后,阵列DacXfr的元素包括归一化的DAC传递函数。
n = 0
FOR i = 0 TO 2N–1
AvgCnt = 0
WHILE i = g[n]
AvgCnt = AvgCnt + 1
DacXfr[i] = DacXfr[i] + u[n]
n = n + 1
IF n >= 2N+3
EXIT WHILE
END IF
END WHILE
IF AvgCnt = 0
EXIT (fail because array, g[ ], is missing a DAC code)
END IF
DacXfr[i] = (DacXfr[i]/AvgCnt)/2N
END FOR
验证
为验证本文所述的办法,运用一台频谱剖析仪来丈量一个14位DAC的输出;该DAC由一个代表抱负正弦波的输入序列驱动。记载了前14次谐波的幅值(2次到15次,单位dBc),并运用这些值重构DAC传递函数f(x)。然后,将抱负正弦输入序列g(t)代入重构的DAC传递函数f(x)进行模仿,发生一个输出序列。一个FFT将u(t)转化为频域等效值U(ω)。从U(ω)提取谐波幅值,并将其与频谱剖析仪的丈量成果比较较,如表1所示。请留意,与7次谐波相关的最大差错仅为0.065 dB。
Table 1
| Harmonic Number | Measured Magnitude (dBc) | Simulated magnitude (dBc) | Deviation (dB) |
| 1 | 0.00 | 0.00 | 0.000 |
| 2 | -75.1 | -75.100 | 0.000 |
| 3 | -74.5 | -74.502 | -0.002 |
| 4 | -90.5 | -90.501 | -0.001 |
| 5 | -86.5 | -86.498 | 0.002 |
| 6 | -92.0 | -91.999 | 0.001 |
| 7 | -95.5 | -95.565 | -0.065 |
| 8 | -93.8 | -93.801 | -0.001 |
| 9 | -97.2 | -97.187 | 0.013 |
| 10 | -89.6 | -89.599 | 0.001 |
| 11 | -94.2 | -94.204 | -0.004 |
| 12 | -98.8 | -98.802 | -0.002 |
| 13 | -95.6 | -95.649 | -0.049 |
| 14 | -99.3 | -99.298 | 0.002 |
| 15 | -91.1 | -91.080 | 0.020 |
因为份额联系,重构传递函数的图形呈现为一条直线(y=x)。现实上,该传递函数与y=x的差错足以发生表1所示的谐波成分。为协助了解,图5仅显现了该传递函数与抱负直线的差错。垂直轴的单位为LSB。