晶振是晶体振荡器的简称。晶体振荡器是指从一块石英晶体上按必定方位角切下薄片(简称为晶片),石英晶体谐振器,简称为石英晶体或晶体、晶振;而在封装内部增加IC组成振荡电路的晶体元件称为晶体振荡器。其产品一般用金属外壳封装,也有用玻璃壳、陶瓷或塑料封装的。

晶振有着不同运用要求及特色,通分为以下几类:一般晶振、温补晶振、压控晶振、温控晶振等。在测验和运用时所供直流电源应没有足以影响其准确度的纹波含量,沟通电压应无瞬变进程。测验仪器应有满足的精度,连线合理安置,将测验及外围电路对晶振目标的影响降至最低。
晶振的分类
依据晶振的功用和完结技能的不同,能够将晶振分为以下四类:
(1) 恒温晶体振荡器(以下简称OCXO)
这类型晶振对温度安稳性的解决方案选用了恒温槽技能,将晶体置于恒温槽内,通过设置恒温作业点,使槽体坚持恒温状况,在必定规模内不受外界温度影响,到达安稳输出频率的作用。这类晶振首要用于各种类型的通讯设备,包含交换机、SDH传输设备、移动通讯直放机、GPS接收机、电台、数字电视及军工设备等范畴。依据用户需求,该类型晶振能够带压控引脚。OCXO的作业原理如下图3所示:
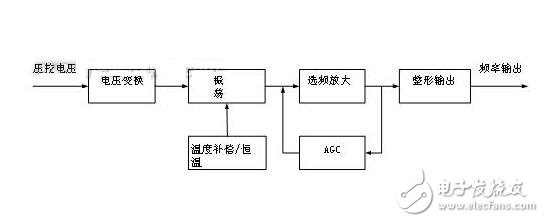
图3恒温晶体振荡器原理框图
OCXO的首要长处是,因为选用了恒温槽技能,频率温度特性在所有类型晶振中是最好的,因为电路规划精细,其短稳和相位噪声都较好。首要缺陷是功耗大、体积大,需求5分钟左右的加热时刻才干正常作业等。我公司出产的此类晶振的典型目标如下:

(2) 温度补偿晶体振荡器(以下简称TCXO)。
其对温度安稳性的解决方案选用了一些温度补偿手法,首要原理是通过感应环境温度,将温度信息做恰当改换后操控晶振的输出频率,到达安稳输出频率的作用。传统的TCXO是选用模仿器材进行补偿,跟着补偿技能的开展,许多数字化补偿大TCXO开端呈现,这种数字化补偿的TCXO又名DTCXO,用单片机进行补偿时咱们称之为MCXO,因为选用了数字化技能,这一类型的晶振再温度特性上到达了很高的精度,而且能够习惯更宽的作业温度规模,首要使用于军工范畴和运用环境恶劣的场合。在广阔研制人员的共同努力下,我公司自主开发出了高精度的MCXO,其规划原理和在世界规模都是抢先的,配以高度自动化的出产测验体系,其月产能够到达5000只,其规划原理如图4。
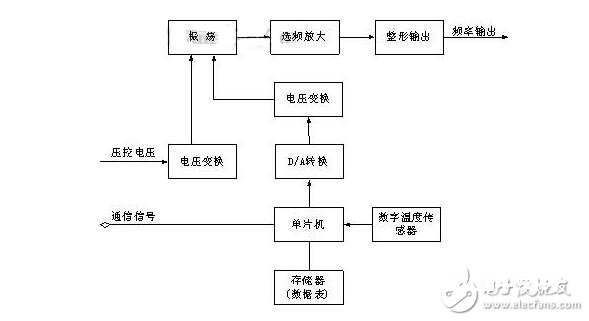
图4 MCXO数字温补晶振原理框图
这类型晶振的典型的使用目标如下:

(3) 一般晶体振荡器(SPXO)
这是一种简略的晶体振荡器,一般称为钟振,其作业原理为图3中去除“压控”、“温度补偿”和“AGC”部分,完全是由晶体的自由振荡完结。这类晶振首要使用于安稳度要求不高的场合。
(4) 压控晶体振荡器(VCXO)
这是依据晶振是否带压控功用来分类,带压控输入引脚的一类晶振叫VCXO,以上三种类型的晶振都能够带压控端口。
晶振的首要参数
1、频率准确度:
在标称电源电压、标称负载阻抗、基准温度(25℃)以及其他条件坚持不变,晶体振荡器的频率相对与其规则标称值的最大答应误差,即(fmax-fmin)/f0;
2、温度安稳度:
其他条件坚持不变,在规则温度规模内晶体振荡器输出频率的最大改动量相关于温度规模内输出频率极值之和的答应频偏值,即(fmax-fmin)/(fmax+fmin);
3、频率调理规模:
通过调理晶振的某可变元件改动输出频率的规模。
4、调频(压控)特性:
包含调频频偏、调频灵敏度、调频线性度。
①调频频偏:压控晶体振荡器操控电压由标称的最大值改动到最小值时输出频率差。
②调频灵敏度:压控晶体振荡器改动单位外加操控电压所引起的输出频率的改动量。
③调频线性度:是一种与抱负直线(最小二乘法)相比较的调制体系传输特性的丈量。
5、负载特性:
其他条件坚持不变,负载在规则改动规模内晶体振荡器输出频率相关于标称负载下的输出频率的最大答应频偏。
6、电压特性:
其他条件坚持不变,电源电压在规则改动规模内晶体振荡器输出频率相关于标称电源电压下的输出频率的最大答应频偏。
7、杂波:
输出信号中与主频无谐波(副谐波在外)联系的离散频谱重量与主频的功率比,用dBc表明。
8、谐波:
谐波重量功率Pi与载波功率P0之比,用dBc表明。
9、频率老化:
在规则的环境条件下,因为元件(首要是石英谐振器)老化而引起的输出频率随时刻的体系漂移进程。一般用某一时刻距离内的频差来丈量。关于高安稳晶振,因为输出频率在较长的作业时刻内呈近似线性的单方向漂移,往往用老化率(单位时刻内的相对频率改动)来丈量。
10、日动摇:
指振荡器通过规则的预热时刻后,每隔一小时丈量一次,接连丈量24小时,将测验数据按S=(fmax-fmin)/f0式核算,得到日动摇。
11、开机特性:
在规则的预热时刻内,振荡器频率值的最大改动,用V=(fmax-fmin)/f0表明。
12、相位噪声:
短期安稳度的频域丈量。用单边带噪声与载波噪声之比£(f)表明,£;(f)与噪声崎岖的频谱密度Sφ(f)和频率崎岖的频谱密度Sy(f)直接相关,由下式表明:
f2S(f)=f02Sy(f)=2f2£;(f)
f—傅立叶频率或违背载波频率;f0—载波频率。









