可控硅整流电路中的波形系数

田太民

某一电压(或电流)的有效值与其均匀值之比，咱们称之为波形系数。在可控硅整流电路中波形系数是个值得留意的问题。为阐明这个问题，咱们先按图1所示的可控硅半波整流电路做个试验，各元件的类型和参数仅供参考。

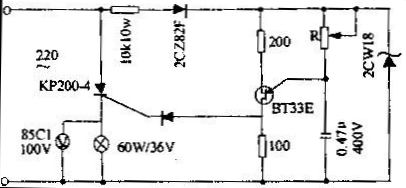
先将R值调至最大，接通电源，此刻直流电压表指示为零，灯泡不亮。然后渐渐减小R值，电压表读数逐步增大，灯泡逐步增亮。咱们会发现当直流电压表指示为10伏时，灯泡便到达正常亮度了，这就是说灯泡的功耗已达额外功率了，若再持续增高电压，灯泡就或许焚毁。为什么电压表的读数还远没有到达灯泡的额外电压36伏，而灯泡的功耗却已到达额外功率了呢?

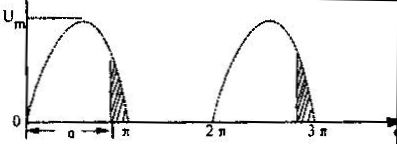
灯火中流过的电流是单向脉动电流，灯泡两头的电压为单向脉动电压，其波形如图2中实线所示。直流电压表的读数是这种脉动电压的均匀值，而刁；是它的有效值。其有效值却要比均匀值大得多。

依据电工学常识，这种周期性的单向脉动电压的有效值U。乃是瞬时值的平方在一个周期内均匀值的算术平方根(均方根值)，即

将不同的Q值代入式(3)，就得到相应的K值，如表一所示。由表一能够看出，当可控硅的移相角由零变到n时，波形系数K值逐步增大，并且增大的速度越来越快，当。挨近，I时，K值将急聚添加(而U和Uo都急聚下降。)

现在再来看看试验成果。据式(2)可算出，当直流电压表指示10伏即U。=10伏时，CO$n=-0．7979，波形系数K~3．57， Uo~35．7伏。Uo己适当挨近灯泡的额外电压了，所以灯泡到达正常亮度。

依据相同的道理可算出，  当G相一起，在电阻性负载的全波可控整流电路中，输出脉动电压(波形见图3中的实线)系数的1／／2倍。在上述核算中，均疏忽了可控硅导通时的正向压降。对其他方式的整流电路以及负载呈电理性时输出电压的波形系数，本文不再赘述。

由上面的剖析可知，在用可控硅进一行整流时，直流电压表(或电流表)上L的读数是输出电压(或电流)的均匀1K值，不能将读数直接代入公式卜U2  L来核算负载上的功耗，这是由于式中U为负载R，上的电压有效值，即U=Uo。

如欲减小波形系数，使输出出电压有效值挨近于均匀值，有三条办法可取：

(1)              尽量减小可控硅的移相角，如Q：o时，则K=I．57(单相半波)：  (2)当负载额外电压比输入沟通电压的有效值低得多时，先用变压器降压再进行整流；  (3)尽量选用单向可控整流或三相可控整流电路。如忽视波形系数的影响，虽然电压表的读数还远未到达负载的额外电压，但仍有或许焚毁电器，致使形成不该有的丢失。这是有必要留意的。

在实践使用中，为便利起见，咱们可依据表二来预算不同的输出直流电压时的波形系数，然后预算出输出电压的有效值。表二中的n为直流电压表的读数U。与输入沟通电压有效值U的比。即    23 (3)，便可得到相应的波形系数K。例如在图1所示的电路中，当直流电压表指示为 50伏时，n=50／220~0．23，依据表二可预算出此刻波形系数K在2．32和1．98之间。

关于全波可控整流电路来说，

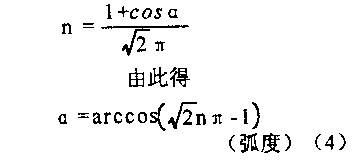
依据相同的道理，可得出全波可控整流电路中，对应于不同n值(可控硅全导通时n获得最大值0．9)时的波形系数K。