当时,非触摸式丈量现已逐步替代触摸式丈量,成为丈量开展的方向。而在各式各样的非触摸式丈量办法中,光纤干与投射技能丈量物体外表描摹的办法,由于其光路具有柔软、形状可变、传输间隔远、抗搅扰能力强等长处,得到了越来越广泛的运用,尤其在各种有强电磁搅扰、易燃易爆等恶劣环境中,光纤干与投射丈量技能更是有着很高的运用价值。
在光纤干与投射技能中,裸露在空气中的光纤简单遭到温度、振荡的影响,使臂长差产生改动,然后产生光相位的改动,导致干与条纹漂移,然后影响到丈量的精度[1]。沟通相位盯梢零差补偿技能(PTAC)是完成光纤相位改动检测和差错补偿的一种关键技能[2],其间触及信号解谐和相位求解,求解反正弦是相位求解的一种首要办法[2]。在FPGA中,传统的求解反正弦函数的首要办法是查找表法[3],查找表数据量的巨细和精度严密相关,在高精度下,查找表法需求很多存储单元,别的也需求校对算法来核算未计入表中的点,这样就对处理器资源提出很高的要求。
针对传统反正弦函数求解办法的缺陷,本文选用CORDIC算法求解反正弦值,得到光相位改动并在FPGA中规划了CORDIC算法完成的流水线结构,然后到达了对光相位改动的实时检测。一起,提出选用查找表合作抛物线插值校对算法处理CORDIC算法在运算中存在的“死区”问题。通过试验验证该了办法的可行性。
1 体系结构
光纤干与投射体系由激光器、聚集透镜和3 dB耦合器等组成。激光器宣布的激光通过聚集透镜耦合到光纤,经3 dB耦合器分光后由两光纤臂输出。两光纤输出端可被看作是杨氏双孔干与中的两个小孔,其输出光由同一点光源宣布,频率相同,具有稳定的相位差,满意杨氏双孔干与条件,然后在输出端产生干与条纹。在实践丈量中,温度、振荡的影响使光纤产生臂长差改动,然后使光相位产生改动,导致干与条纹漂移。为处理这一问题,通过PTAC对光相位进行调制解调得到光相位改动信息并对相位差错进行补偿。
如图1所示,光纤干与投射沟通相位盯梢零差补偿体系由激光器、聚集透镜、3 dB耦合器、PZT和信号调度等部分组成。两输出臂别离缠绕在两个PZT上,一路作为信号臂对光相位进行调制,另一路用作操控和补偿。两条输出臂投射端面存在反射,反射的光返回到3 dB耦合器中产生干与,构成马赫-泽德干与仪[4],干与的光由光电探测器PD接纳。信号臂反射回耦合器的光包括光相位调制信息,一起也存在着由环境影响产生的光相位改动信息。两束反射光在耦合器中产生干与,则光相位调制信息转化为光强改动,再由光电探测器将光强改动转化为电信号。

通过AD转化后,输入FPGA进行核算,通过求解反正弦求出?琢。改动驱动器的直流偏置,即改动待测镜和参阅镜的相位差?琢。再通过数模转化、高压扩大,通过操控PZT2调整另一输出臂的长度,使两光纤臂相位差坚持为一正弦函数,消除温度振荡等环境要素带来的影响。
2 反正弦算法完成
2.1 反正弦算法原理
依据CORDIC算法核算反正弦。数字信号处理中常常会遇到求解逾越函数的问题,如求解矢量旋转、反三角函数运算、双曲函数等,CORDIC是为了这些问题而提出的[5]。CORDIC基本思维是用一组确认的视点不断摆偏去迫临所求的视点,而这一组视点与运算基数(2i)有关。在硬件电路中,CORDIC运算能够只通过加减操作和移位操作完成,大大节省了资源。CORDIC算法可由式(3)、(4)、(5)、(6)给出[6]。其间,(xi,yi)是矢量的坐标,zi为剩下未旋转的视点。
2.2 反正弦程序规划
2.2.1 字长规划
输入值规模为[-1,1],输入FPGA的初值c为12位。选第一位为符号位,第二位为整数位,后10位为小数位。在FPGA中,运用浮点方式核算小数比较复杂,因而,将小数部分左移10位,化成定点方式运算。CORDIC的核算次数取决于xi、yi的小数位数。如式(8),用yi与输入初值c比较,假如yi的小数位为10位,则最多进行10次CORDIC核算,精度很难确保。因而,规划xi、yi的小数位为22位,在c后边补0,补足22位小数位,则最多可进行22次CORDIC核算。由于z的值域规模为[-1.570 8 rad,1.570 8 rad],将z规划成25位,z[24]为符号位,z[23:22]为整数位,z[21:0]为小数位。
2.2.2 完成结构的规划
在FPGA中,CORDIC的完成结构能够挑选迭代结构或流水线结构。迭代结构是直接由公式写出循环句子,处理完当时数据才能够处理下一个数据,缺陷是功率低。本规划选用流水线结构,流水线结构在数据处理的一起,还能持续输入和处理后续数据,进步了数据吞吐率。此外,规划中选用前端数据处理加22级CORDIC核算加后端处理,第一个数据需求24个时钟周期处理完毕,之后每个周期都能够输出一个处理成果,能够明显进步数据处理速度。
2.2.3 CORDIC结构
本规划总共有22级CORDIC核算模块,第i级CORDIC核算模块如图3所示。yi与|ci|比较,决议di的值,再依据式(7)来核算xi+1、yi+1、zi+1,一起传递输入值的符号位,在流水线的后端处理模块处理。若输入c[11]为1,则成果为-arcsinc;若输入c[11]为0,则成果为arcsinc。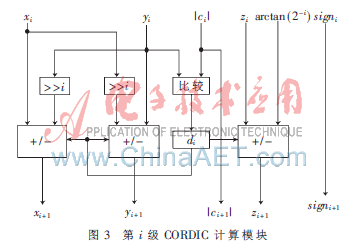
3 算法校对
输入数据规模为[-1,1],将核算成果与实在成果比较,得到差错散布如图4所示。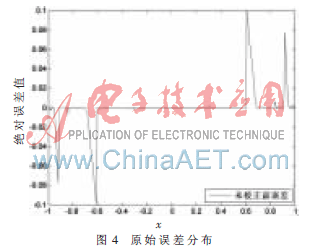
由图4可见,在横坐标绝对值为0.6、0.8、0.9邻近呈现较大差错,最大差错到达10-1数量级。CORDIC算法运用的是一种数值核算迫临的思维,增减的步长值是离散的,为arctan(2i)。在横坐标绝对值为0.3、0.6、0.8、0.9邻近,CORDIC核算存在“死区”。本文选用查找表和抛物线插值校对,在差错值较大的区间[c1,c3],令:
在前端数据处理中判别输入值是否在需求校对的区间,若在则进行抛物线插值校对。用少数查找表存储校对区间端点的反正弦值和分母的比值。选用FPGA为32 bit,在其间规划乘法运算时,乘数和被乘数最高为16 bit才不会使数据溢出。在所有抛物线插值校对系数中,区间[0.95,0.96]上抛物线插值校对的一次项系数最大为22.108 9。因而挑选高5位为整数位,低11位为小数位进行运算。
4 试验与仿真
CORDIC程序流程图如图5所示,初始化之后,先判别输入值c是否在需求校对的区间。若是,则进入抛物线插值校对运算;不然进行CORDIC运算,使x0=1/An,y0=0,z0=0。CORDIC运算核算出一个小数的反正弦值需求24个时钟周期,为了确保流水线的机能,当输入值c在需求校对的区间时,插值核算后的数据在CORDIC运算模块中直接传输。核算出反正弦值后,判别输入值c的符号位,假如是0,则c为正数,反正弦值也为正数;假如是1,则c为负数,反正弦值也为负数。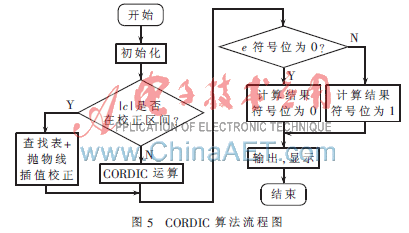
仿真软件选用ModelSim SE PLUS 6.2b。输入的c值规模为[-1,1],存放在ModelSim的测验鼓励文件中。处理一个数据需求24个时钟周期,之后每个周期都能输出一个数据,如图6所示。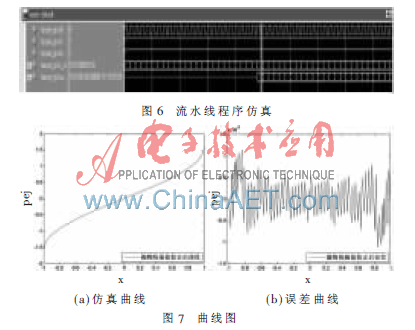
将仿真后的数据导入Matlab得到反正弦仿真曲线,如图7(a)所示,并与抱负值比照,得到如图7(b)所示差错曲线,CORD%&&&&&%核算部分弧度值精度到达10-4数量级,通过校对的部分,差错从10-1数量级降到10-4数量级。
本规划选用流水线结构,进步了数据吞吐率。仿真试验标明,光相位的差错精度到达10-4数量级,精度较高,且具有较高的运算速度,合适大数据量高速处理。