物尽其用，10大办法教你扩展示波器用处

现有示波器的一些非传统运用能够让你扩展这种通用仪器的用处。你为示波器支付了大笔费用，你应该充分发挥它的价值。本文总结了十个或许令你惊讶的示波器运用。其间任何一个运用你都会发现十分有用。 现在的中档示波器具有的功用实际上比大大都工程师曾用过的要多。本文总结了十个或许令你惊讶的示波器运用。其间任何一个运用你都会发现十分有用。 运用示波器的快速边缘功用和数学运算完结频率呼应测验 频率呼应丈量需求具有平整频谱的信号源。经过将示波器的快速边缘测验信号用作阶跃信号源，再运用示波器的衍生功用就能够得到待测设备的脉冲呼应。然后运用快速傅里叶变换(FFT)功用取得频率呼应。图1显现了取得输入信号的频率呼应和37MHz低通滤波器的频率呼应的进程进程。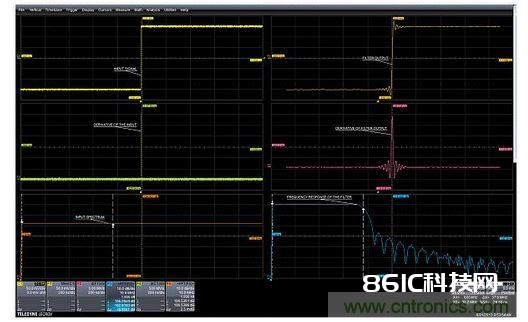
图1：先将快速边缘测验信号加到滤波器的输入端(左上)，然后用滤波器输出(右上曲线)对它进行微分(右中)，终究求FFT的均匀值(下右)，就能够得到滤波器的频率呼应。左下边曲线中的频谱展现了微分过的阶跃输入信号的频率平整度。 快速边缘测验信号的上升时刻约为800ps，带宽约为400MHz，比这次丈量的100MHz规模大得多。 运用示波器的低通数字滤波器对输入信号进行高通滤波 假如你的示波器能够运用比如增强分辨率(ERES)数学函数等功用对信号进行低通滤波，那么你就能对相同的信号进行高通滤波。留意，只要你能拜访数字低通滤波器的输入和输出端时这个功用才干完结。图2显现了详细完结进程。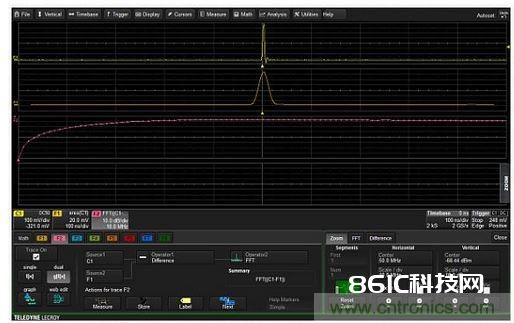
图2：从输入信号(C1，顶部曲线)中减去低通滤波后的波形(中心F1曲线)构成的信号就具有高通特性，如数学曲线F2(底部曲线)的频谱所示。 输入信号曲线C1是一个很窄的脉冲。数学曲线F1(中心曲线)运用示波器的ERES数字滤波器对C1信号进行滤波。从输入信号中减去滤波器曲线后构成的信号就只要较高频率的成分。曲线F2履行减法操作，一起完结高通信号的FFT，因而你能看到高通特性。低通呼应跌至最大呼应0.293处的频率便是高通滤波器的-3dB点。只对具有特定形状或丈量参数的信号进行均匀 能够依据波形模板或参数化丈量供给经过/失利测验、并能将满意经过/失利规范的波形存储到内存中的示波器能够有挑选地将这些波形加入到示波器的均匀功用中。要启用这项功用，首要要依据波形模板和/或处于方针极限内的丈量参数输入经过/失利规范。针对经过的测验，要将波形存储到内部的存储器中。发动均匀功用对该内存中的内容进行均匀。成果是只要满意测验规范的波形才会加到均匀内容中。图3显现了这样一个完好的进程。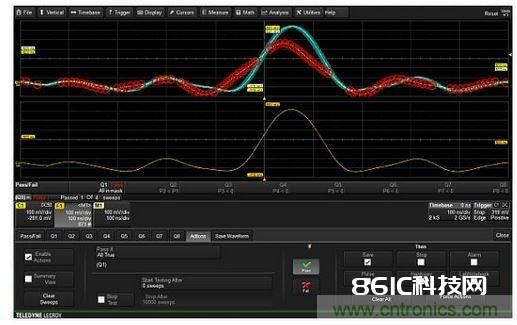
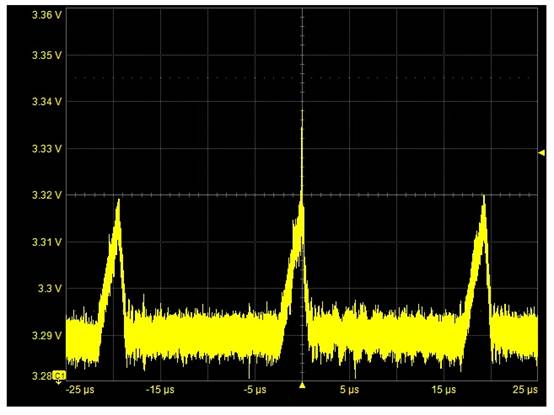
图3：只对波形模板中包括的那些波形进行有挑选的均匀。通道1曲线(C1)与模板不匹配，赤色圆圈指出了坐落模板外的区域。终究承受的曲线被存储在内存曲线M1中，整个曲线都坐落模板之内。数学曲线F1显现的累加均匀曲线仅仅将落入模板中的波形进行了均匀累加。 经过/失利测验是经过彻底落入模板内的波形(蓝色显现)的一种测验。满意经过规范的波形被存储在内存M1中，并添加到功用曲线F1中的均匀曲线中。不满意规范的波形会被丢掉，永久不会呈现在均匀曲线中。 经过运用排它型触发器只捕获反常事情来寻觅间歇性事情 智能或先进的触发器能够依据宽度、周期或占空比等选定的波形特征进行触发。有几家制造商的产品还能依据处于规模之内或规模之外的智能触发事情进行触发。这种触发器便是排它型触发器，它能够用来只对反常事情进行触发，如图4所示。在这个比如中，示波器被设置为只对宽度超越48±0.8ns的脉冲进行触发。在遇到宽度为52.6ns的大脉冲产生之前这种触发器是不会触发的。因为示波器只对宽度超越标称值为48ns的脉冲进行触发，因而不存在改写速率的问题。平常它就处于”等候”状况，直到反常脉冲宽度呈现。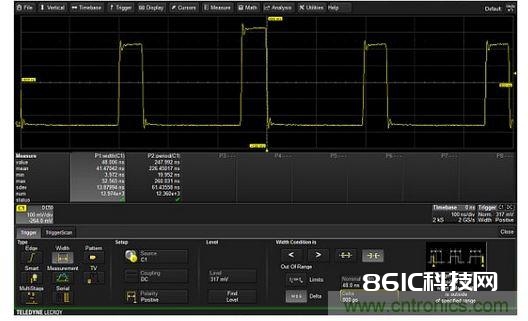
图4：只对脉冲宽度超越48±0.8ns规模的脉冲触发的排它型触发器。因而示波器只在遇到52.6ns的大脉冲时才被触发，一切正常的48ns宽度脉冲都被示波器所疏忽。将趋势函数和触发器延时用作自定时数据记录器 趋势图是按收集的次序显现的被测参数值图形。图5便是这样一个比如。比如中选用灵敏度为39μV/℃的热探头丈量振荡器的内部温度。与此一起取得在单个周期内得出的频率。每个趋势中的100次丈量都是经过100次收集得到的。触发源是振荡器的输出。正常状况下这会导致示波器以其标称改写率进行触发。为了避免产生这种现象，并且在两次丈量之间设置已知的延时，能够运用触发器延时功用。运用触发器延时功用能够将两次收集之间的时刻设为10秒，因而总的丈量距离是1000秒。再用参数化数学调整函数将温度传感器的电压读数转换为摄氏度。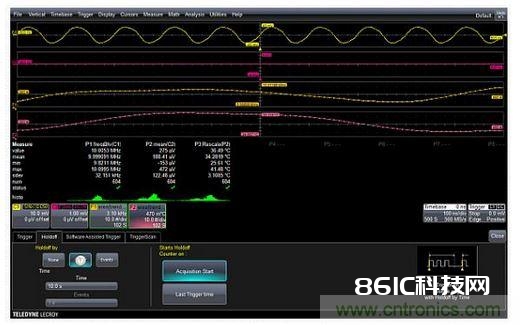
图5：在1000秒时刻内收集到的内部温度(曲线F2)和振荡器输出频率(曲线F1)的趋势图，它反映了振荡器的热呼应特性。 解调起伏调制信号 起伏调制(调幅)信号的包络检测办法需求对信号进行峰值检测。峰值检测能够经过整合绝对值数学函数和这种示波器中称被增强分辨率(ERES)的数字低通滤波器来完结。这样能使精确地提取调制包络形状变得十分简略。图6显现了一个比如。左上边的曲线是待收集的调幅信号。绝对值数学函数的运用如左下边的曲线所示，绝对值供给全波整流作用。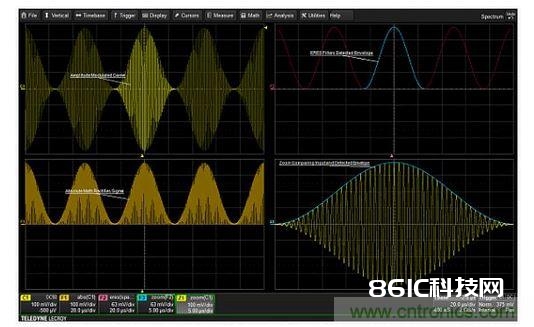
图6：从调幅信号中提取调制包络的进程。绝对值用于检测信号。ERES滤波能够消除高频载波，然后产生洁净的调制包络。 稀少函数和ERES函数组合用于对绝对值进行低通滤波，构成如右上边曲线所示的调制包络。 稀少函数能够有挑选地削减收集波形的采样率，因而有助于设定作为采样率函数的ERES低通滤波器的截止频率。低通滤波器的截止频率有必要远小于载波频率。 右下方格子中的曲线是输入调幅信号的掩盖缩放曲线，提取出的包络显现了该进程的保真性。接下来就能够直接对提取出的包络进行丈量和进一步剖析。 检测频率、相位和脉宽调制的信号 许多中档示波器都具有轨道或时刻趋势功用，能够依据被测时序参数的周期性改变产生波形。轨道功用在时刻上与源波形是同步的，因而很简略将频率、宽度或相位的改变与源波形相关在一起。这样就供给了解调调频(FM)、调相(PM)或脉宽调制(PWM)信号的一种办法。图7显现了运用时刻距离差错(TIE)参数的轨道解调调相(PM)波形的一个比如。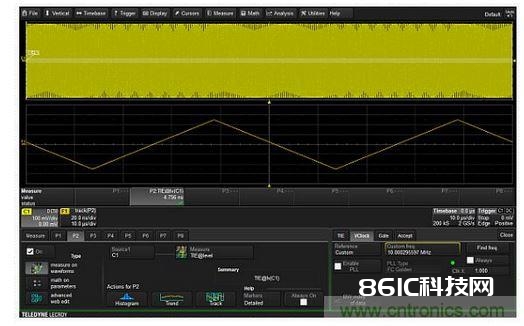
图7：运用TIE参数轨道能够制作出PM波形每个周期的瞬时相位与时刻的联系图，然后完结对调相信号的解调。 TIE是跨过波形的阈值与跨过抱负方位的阈值之间的时刻差。实际上它便是信号的瞬时相位。因而TIE轨道显现了载波相位的周期性改变，能够用来产生相位改变在时刻上与原始调制载波同步的波形。图中的笔直刻度是时刻单位，经过简略的调整操作很简略转换为相位。相同，频率参数轨道能够显现调频载波的调制信号，脉冲宽度轨道能够产生PWM解调。向示波器的快速傅里叶变换添加”最大值坚持”功用 频谱剖析仪供给的峰值或最大值坚持功用在扫正弦频率呼应丈量时十分有用。大大都示波器的FFT没有供给这个功用，但它们供给最高或最大数学函数，与FFT结合起来就能够坚持FFT中每个频率单元点产生的最大起伏。图8供给了该功用的一个比如。
图8：赤色曲线F2(中心)显现了扫频正弦波FFT中的每个频率的峰值或最大值。曲线F1(底部)是没有运用最高或最大值的FFT。F2描述符盒子显现了最高功用的设置。 当输入正弦波在整个频率规模内扫描时，曲线F2中显现的最高(或最大)函数将坚持FFT中每个频率单元点的峰值起伏，因而答运用户看到每个频点的最大呼应。 核算单位为V2/Hz的波形功率谱密度 示波器FFT用对数方式的dBm和dBm/Hz为单位别离显现功率谱和功率谱密度(PSD)。而比如噪声剖析等运用要求选用V2/Hz或V/√Hz等线性单位的功率谱密度。经过运用少数的FFT和从头调整数学函数运算就能够完结线性刻度的功率谱密度丈量。图9显现了这种丈量的FFT设置。FFT输出类型被设为平方量级，以便用笔直单位V2显现FFT。转换到功率谱密度要求FFT归一化为FFT的有用分辨率带宽，也即分辨率带宽(Δf)和所选加权函数的有用噪声带宽ENBW的乘积，详见图9中FFT设置的陈述。
图9：曲线C1是捕获到的频带受限的噪声信号。曲线F3是线性笔直刻度单位为V2/Hz的功率谱密度。参数P7读取功率谱密度曲线下方的面积，并与时刻波形的均方值进行比较，后者是以参数P8中的曲线C1的规范偏差平方值核算的。 这种示波器将FFT读作峰值，因而咱们还有必要将这个值转换回均方值，这意味着将一切起伏值除以2。归一化是用从头调整数学函数完结的，在本例中是将每个FFT起伏值乘以5×10-6。成果曲线如图9中的F3所示，读取的 功率谱密度的单位是V2/Hz。参数P2是输入波形C1的规范偏差。这个值在参数P8中进行了平方，是输入信号的均方起伏。参数P7读出功率谱密度曲线(F3)下方的面积为23.3mV2。它也陈述均方起伏–在本例中从FFT得出的值为23.28mV2，用于承认这个进程。运用缩放选通式FFT比较频谱重量 偶然你或许需求对捕获波形的一小部分履行FFT。这种状况通常是有疑问波形在时刻上产生改变时产生的。大大都示波器答应你经过FFT操控中的选通功用或在捕获波形缩放基础上核算FFT来选通FFT进程。记住，不管是哪种状况，FFT分辨率带宽都将被确定为选通信号持续时刻的倒数。因为选通部分短于整个波形，分辨率带宽将添加，FFT频率分辨率将下降。图10显现了对一个线性正弦扫描波形进行选通式FFT剖析的比如。正弦波的频率在10ms扫描时长内从1MHz改变到80MHz(左上边的曲线M1)。 在437μs和1.42ms点收集了两个时长为5μs的缩放波形(左中是曲线Z1，左下是Z2)。整个波形的FFT(右上的F1)显现在整个扫描规模内具有一致的起伏。Z1和Z2的FFT显现了扫描进程中在所选时点的频率。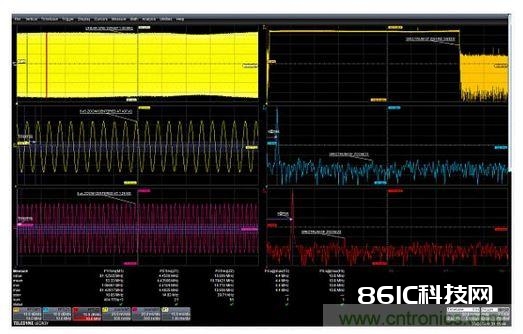
图10：运用缩放功用选通FFT的比如。在437μs和1.42ms处收集的两个5μs缩放波形显现了作为时刻函数的频率的不同。 本文小结 现有示波器的一些非传统运用能够让你扩展这种通用仪器的用处。你为示波器支付了大笔费用，你应该充分发挥它的价值。走运的是，上述这些技巧有助于你做到这一点。