1 导言
在暗码学范畴,使用暗码技能|0″>暗码技能对传输信息进行加密发送、解密接纳,是一种卓有成效的办法。暗码学开展至今已有许多优异的算法创造并得到使用,例如私钥暗码体系中的DES暗码、IDEA暗码、序列暗码;公钥暗码体系中的RSA暗码、椭圆曲线暗码等,他们各有规划特色和对应的使用范畴,其间序列暗码一直是暗码学中最重要的加密办法之一。使用组合LFSR序列作为序列暗码的前馈电路,可充分使用m序列的杰出核算特性和加大输出序列周期和线性杂乱度的优势,但如安在确保前馈电路输出核算特性不被损坏的基础上,置换与紊乱输出联系,增强暗码的保密性仍是该范畴研讨有必要考虑的问题。传统办法是使用非线性函数对前馈电路输出进行改换,但在函数规划与生成速度上限制了其开展;使用某LFSR序列发生操控信号去操控并行LFSR序列,这种方式电路如Geffe发生器、Jenning发生器、交织停走式发生器等,易遭到相关性进犯,应防止在保密强度要求高的部分使用。跟着现代科学技能的开展,将神经网络、混沌等算法融入暗码学的研讨已不断深入,伴跟着数字化技能和大规模集成电路的快速开展,一些算法不只中止在理论研讨与模仿仿真试验上,使用硬件电路进行规划并完结已逐步成为事实。怎么衡量加密芯片的杂乱度是应该研讨的问题,当加密芯片被敌方得到并破译时,以高杂乱度坚持加密信息的安全性是加密芯片成功规划的要害。现提出一种混沌组合序列暗码杂乱度剖析与规划办法,并由此规划混沌组合序列暗码电路并依据FPGA完结。
2 序列暗码原理
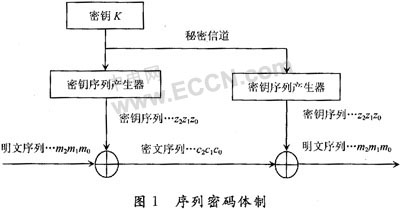
因为语音、图画和数据等信息都可以经过量化编码转化为二进制数字序列或自身便是二进制数字的序列,因此可以假定序列暗码体系中的明文为二进制数字序列组成的调集m={mi},密钥空间为K,密文空间为C={ci}。如图1所示,关于每一个k∈K,由算法Z可以确认一个二进制序列Z(k)=z0,z1,z2,…,当明文为m0,m1,m2,…,mn-1时,在密钥k下的加密进程为:对i=1,2,3,…,n-1,核算ci=mi○+zi,密文为c=Ek(m)=c0,c1,c2,…,cn-1,对密文c的解密进程是:对i=1,2,3,…,n-1,核算mi=ci○+zi,由此康复明文为m。一般,称密钥k为种子密钥,由k经过算法Z发生的序列Z(k)称为密钥序列。
由此可见,序列暗码的安全性首要取决于密钥序列Z(k)和序列暗码算法的难破译性。当z0,z1,z2,…为均匀分布的二进制随机序列时,则该暗码体系为一次一密体系,因此是不行破的。可是因为Z(k)是一个由k经过确认性算法发生的伪随机序列,所以该暗码体系的保密性要害是高杂乱度规划。
3 暗码芯片电路规划
依据国内外在混沌序列暗码研讨的剖析,本文规划了依据FPGA的混沌序列暗码芯片,该芯片中心部分是混沌序列暗码模块,如图2所示。加密芯片除混沌序列暗码模块外还有操控模块和加/解密传输模块。

从该框图可以看出,由8个LFSR序列作为驱动源,Lorenz混沌体系与数据挑选器Ⅰ构成对8个LFSR序列进行非线性改换部分,数据挑选器工输出序列与数据挑选器Ⅱ输出序列相异或后发生密钥输出序列。
挑选器依据Lorenz混沌体系挑选信号输出,其间挑选器的操控端信号也来源于Lorenz混沌体系的恣意一输出。依据多个LFSR序列作为驱动源的特性得知,当LFSRi(i=1,2,…,n)的级数N1,N2,…,Nn两两互素且满意必定条件时,该组合序列输出周期为。为了使输出序列有尽或许大的线性杂乱度,各Ni应尽或许挨近N/n,其间N=N1+N2+…+Nn。当Ni确认今后,为使每个LFSRi(i=1,2,…,n)生成周期为2Ni-1的m序列,其充要条件是使其特征多项式为来源多项式。
4 暗码芯片电路的杂乱度剖析
该结构输出周期较单一LFSR作为前馈电路的输出周期大大添加,一同此电路的杂乱度大大添加,可从以下证明中得到。
该暗码电路中构成线性杂乱度的首要器材有8个LFSR、混沌序列发生器及数据挑选器,设8个LFSR级数别离为Di(i=1,2,…,8)且互不持平,di(i=1,2,…,8)别离为8个LFSR的输出,a0a1a2为Lorenz混沌序列输出,设Y1(t),Y2(t)别离为数据挑选器Ⅰ和Ⅱ的输出,那么:
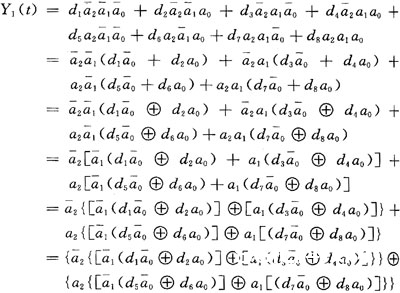
假如假定混沌每个输出序列杂乱度为A,LFSR的杂乱度别离以他们各自级数表明,依据杂乱特性根本定理,则Y1(t)的线性杂乱度L1可由上面的逻辑输出表达式核算为:

此式给出描绘多操控端的数据挑选器线性杂乱度的根本公式,可看出该电路线性杂乱度首要由An项决议,假如LFSR数目添加,杂乱度将为幂指数增加。
5 加密芯片电路输出测验
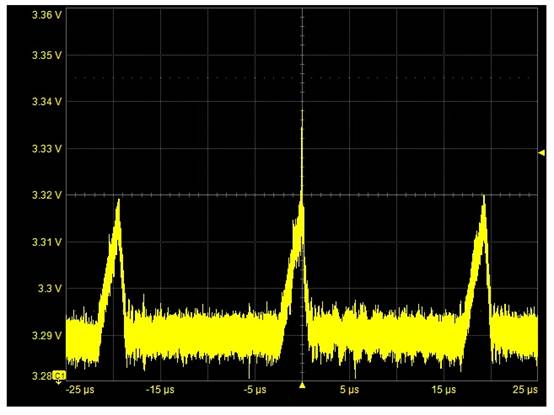
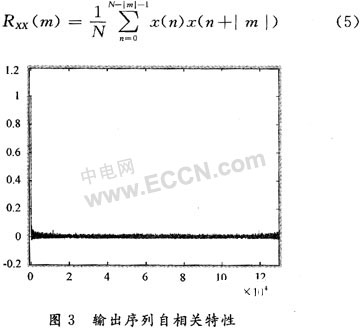
使用ALTERA公司的QuartusⅡ东西和方针芯片EP20K300EQC240规划,对逻辑归纳成果进行仿真后完结硬件下载功用。为验证其输出序列的平衡性、相关性及游程等特性,对下载后输出序列使用Agilent1693A逻辑剖析仪进行数据测验、存储并使用Matlab进行核算剖析。在实践使用中,假如平稳随机序列满意各态历经性,核算均值可用时刻均值替代。取一个有限的核算体系可以接受的时刻均值和时刻自相关序列,并用他们作为核算均值和核算自相关序列的估值。依据此理论设定一初始数据,在一段时刻内观测其输出序列的平衡性、游程性、自相关性及互相关性,根本满意暗码序列输出要求,现以自相关特性测验为例进行阐明。
将混沌组台序列转化成X={x(n)|n=0,1,2,…,x(n)∈{-1,1}},使序列输出概率密度关于0对称。取测验序列N=12×104,并使用自相关函数的估值式(5)进行仿真,得到该神经网络序列的自相关特性如图3所示。可看出该暗码序列输出具有较好的自相关特性,在0值处峰值尖利,其他值近似为0,类似于δ函数。
6 结 语
该电路的特色为:
(1) 单个混沌体系对多LFSR进行非线性改换,无限延拓多LFSR周期,在极大扩展了周期空间的一同,又添加了序列的杂乱性;
(2) 由LFSR序列和混沌序列一同构建加密芯片电路的规划,防止由单一混沌序列而被重构的或许;
(3) 此电路的杂乱性将高于单一混沌电路,更远高于由LFSR组合序列生成电路;
(4) 该电路用FPGA技能进行规划,使硬件电路与数学算法有机结合一同,FPGA技能的特色使所规划电路易移植和更改,这对暗码的规划非常有利。
此加密芯片经VHDL规划并生成,整个时序由状态机操控,逻辑联系契合电路规划要求。此研讨成果有助于加速混沌序列暗码芯片的研讨与使用,使加密算法更灵敏有效地使用到信息安全和现代保密通讯设备中。