快速傅里叶改换(FFT)作为核算和剖析东西,在很多学科范畴(如信号处理、图画处理、生物信息学、核算物理、使用数学等)有着广泛的使用。在高速数字信号处理范畴,如雷达信号处理,FFT的处理速度往往是整个体系规划功用的关键所在。
针对高速实时信号处理的要求,软件完成办法明显满意不了其需求。近年来现场可编程门阵列(FPGA)以其高功用、高灵活性、友爱的开发环境、在线可编程等特色,使得依据FPGA的规划能够满意实时数字信号处理的要求,在市场竞争中具有很大的优势。
在FFT算法中,数据的宽度一般都是固定的宽度。但是,在FFT的运算过程中,特别是乘法运算中,运算的成果将不可防止地带来差错。因此,为了确保成果的准确性,选用定点剖析是十分必要的。
1 FFT算法原理
FFT算法的基本思想便是使用权函数的周期性、对称性、特殊性及周期N的可互换性,将较长序列的DFT运算逐次分解为较短序列的DFT运算。针对N=2的整数次幂,FFT算法有基-2算法、基-4算法、实因子算法和割裂基算法等。这儿,从处理速度和占用资源的视点考虑,选用基-4按时刻抽取FFT算法 (DIT)。关于N=4γ,基-4 DIT具有log4N=γ次迭代运算,每次迭代包括N/4个蝶形单元。蝶形单元的运算表达式为:
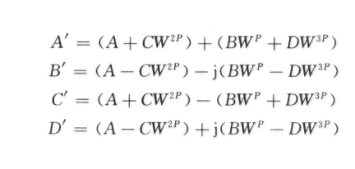
其信号流如图1。式中:A,B,C,D和A′,B′,C′,D′均为复数据;W=e-j2π/N。进行1次蝶形运算共需3次复乘和8次复加运算。N=64 点的基-4DIT信号流其输入数据序列是按天然次序排列的,输出成果需经过整序。64点数据只需进行3次迭代运算,每次迭代运算含有N/4=16个蝶形单元。
2 FFT算法的硬件完成
2.1 流水线办法FFT算法的完成
为了进步FFT作业频率和节约FPGA资源,选用3级流水线结构完成64点的FFT运算。流水线处理器的结构如图2所示。
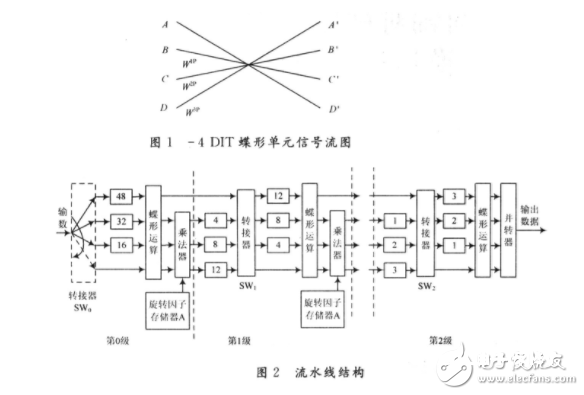
每级均由延时单元、转接器(SW)、蝶形运算和旋转因子乘法4个模块组成,延时节拍由方框中的数字表明。各级转接器和延时单元起到对序列进行码位抽取并将数据拉齐的效果。每级延时在FPGA内部用FIFO完成,不需求对序列进行寻址即可完成延时功用。数据串行输入,经过3级流水处理后,串行输出。
转接器有必定的作业规矩。例如,当第0级改换做完进入转接器SW1前,先对后三路数据进行必定节拍的延时,推迟节拍分别为4,8,12。为了阐明规矩,把输入转接器的四路数据依照前后次第进行分组,每4个时钟节拍为1组,共16组,如图3(左)所示。在数据流串行经过转接器SW1时,第0组中的数据坚持不变,第1组中的数据与第4组中的数据交流;5不变,2和8交流,3和12交流,6和9交流;10不变,7和13交流,11和14交流,15不变。交流完毕后,前三路数据经过推迟节拍分别为12,8,4的FIFO存储器输出,方位联系如图3所示。\
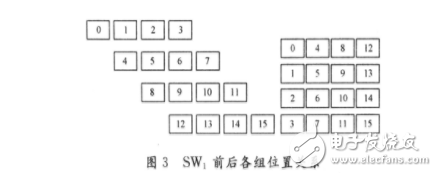
上述转化规矩关于SW2也是适用的,仅仅转接器前后的延时节拍和分组的巨细有所不同。
2.2 存储单元
为了完成算法的流水线规划,存储器RAM规划为64×16 b的双端口RAM,即在时钟信号和写操控信号一起为低电平时,从输入总线写入RAM;在时钟信号和读操控信号一起为高电平时,从RAM输出数据。
ROM为17×16 b的ROM,贮存经过量化后的旋转因子,旋转因子为正弦函数和余弦函数的组合。依据旋转因子的对称性和周期性,在使用ROM存储旋转因子时,能够只存储旋转因子的一部分。
2.3 运算结构
Radix-4蝶形运算单元是整个FFT处理器中的核心部件。在用Radix-4运算器核算时需求并行输入数据,假如能以并发数据输入的话,则同步性和操控度较好,但实际上常要进行串并之间的转化。存储RAM按单节拍输出16 b位宽数据,选择器不断旋转送入到确认的方位,每4点悉数到位后R-4使能有用;然后4个时钟节拍得到有用成果数据,再经过选择器旋转送入到对应存储 RAM中。
复数运算中,对应复数的实部和虚部RAM用同一个地址产生器。地址产生器在进行RAM地址产生时选用两套地址,第一套是计数器按时钟节拍次序产生的,用于输入数据的存储;第二套是由数据宽度为16 b的ROM产生的,ROM中寄存的数据为下级运算所需倒序的序列地址,产生地址给RAM,然后RAM按倒序地址输出下级需求进行运算的数据。
2.4 块浮点结构
数字信号处理体系可分为定点制、浮点制和块浮点制,它们在完成时对体系资源的要求不同,作业速度也不同,有着不同的适用规模。定点制算法简略,速度快,但动态规模有限,需求用适宜的溢出操控规矩(如定份额法)恰当紧缩输入信号的动态规模。浮点表明法动态规模大,可防止溢出,但体系完成杂乱,硬件需求量大,速度慢。
为了进步精度,并削减杂乱度和存储量,选用块浮点结构。块浮点算法是以上两种表明法的结合。这种表明办法是,一组数共用同一个阶码,这个阶码是这组数中最大数的阶码。块浮点算法无需进行额定的指数运算,仅对尾数进行运算即可,其与定点运算相同便利,但需求在每级运算完毕后进行本级运算溢出最大位数判别,以对数据块进行块指数调整。在调整时仅保存一位符号位,因此能够充分使用有限位长。这样处理比定点办法扩展了动态规模,而且进步了精度,比浮点运算在速度上有了进步。块浮点结构如图4所示。
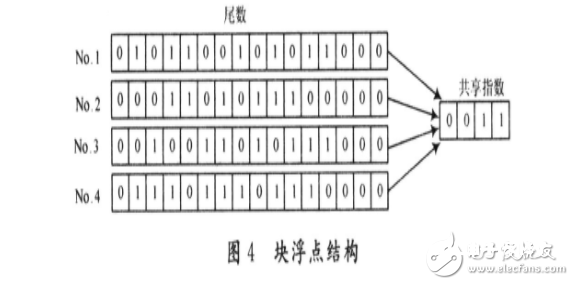
3 结 语
侧重评论依据FPGA的64点高速FFT算法的完成办法。选用高基数结构和流水线结构,大大进步了FFT处理器的运转速度。一起块浮点结构的引进,也大幅削减了浮点操作占用FPGA器材的资源数目,统筹了FPGA高精度、低资源、低功耗的特色。从试验成果看,该办法能够满意高速实时处理数字信号的要求。