1、 功率放大器回忆效应发生原因及影响
功率放大器非线性特性发生的失真重量不稳定,例如三阶或五阶交调的崎岖、相位会随输入信号崎岖和带宽的改动而改动。这种失真重量依赖于输入信号崎岖、带宽的现象一般称之为功率放大器的回忆效应。
细微的回忆效应自身对功率放大器的线性度并无严重影响。即在双音频测验中,跟着音频距离的添加,假如放大器三阶交调重量的相位旋转不超越10o,且崎岖崎岖不大于0.5dB,此刻功放的回忆效应不会明显影响附近信道功率比,能够不予考虑。但是,当功率放大器的上下边带的ACPR(an adjacent channel power ratio,相邻信道功率比)呈现较大不对称现象时,即便三阶、五阶交调重量的相位和崎岖失真很小,也不能疏忽回忆效应对放大器的影响。
2 、削弱功放回忆效应的根本思路
功放回忆效应使射频预失真线性化功率放大器的效果有很大退化,为增强射频预失真线性化功率放大器的稳定性和可靠性,需对所规划的功率放大器进行削弱回忆效应的相关处理。
下降回忆效应的根本主意是:经过附加电路滤除由包络和二次谐波操控的三阶交调重量。最简洁的办法是在四分之一波长传输线后边的偏置线上,添加辅佐电路使包络信号和二次谐波短路,但因为传输线的离散效果,使得这种办法难以完成宽带短路。因而,短路电路网络应当直接加在紧靠栅极和漏极的当地,而不用经过四分之一波长传输线才短路。短路网络可运用LC串联电路完成。
3、 选用附加电路法削弱功放回忆效应剖析
运用附加电路滤除由包络和二次谐波操控的三阶交调重量,对减小功率放大器的回忆效应是有用的,现剖析如下:
假定信号的中心频率为f_{0}、带宽为f_{U}-f_{L},并带有二次谐波和包络重量。它的频谱如图1所示。
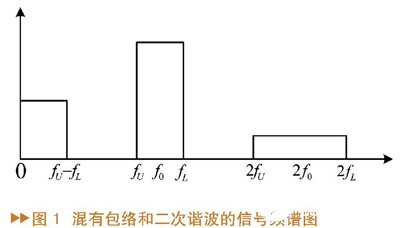
信号的中心频率可表示为
f_{0}=\frac{f_{U}+f_{L}}{2}≈\sqrt{f_{U}f_{L}} (1)
晶体管的一种抱负输出端口匹配电路拓扑如图2。
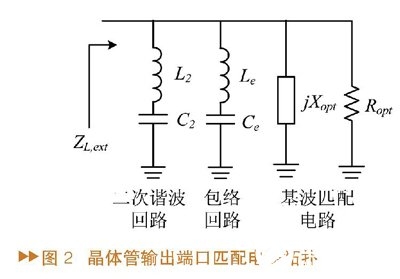
输入端口的匹配电路拓扑相同选用上面的结构。图中包括滤除二次谐波和包络的LC谐振回路和基波的最优匹配电路。为了使滤除二次谐波的LC谐振回路对二次谐波2f_{U}和2f_{L}具有相同的阻抗,则L2与C2组成的谐振回路须在频率2\sqrt{ω_{U}ω_{L}}处振动,即
L_{2}C_{2}=1/(4ω_{U}ω_{L})≈1/(2ω_{0})^{2} (2)
假定滤除包络的LC谐振回路和基波匹配电路的阻抗在二次谐波频率处十分大,则输出负载阻抗Z_{L},_{ext}(2f_{U})和 Z_{L},_{ext}(2f_{L})是共轭的,它们的模为
∣Z_{L,ext}(2f_{U})∣=∣Z_{L,ext}(2f_{L})∣=4πL_{2}(f_{U}-f_{L}) (3)
明显,Z_{L,ext}(2f_{U})和Z_{L,ext}(2f_{L})与电感L2和信号带宽有关。
为了将包络信号短路,须运用一个大电容Cg。相同地,假定滤除二次谐波的LC回路和基波匹配电路在信号带宽频率处的阻抗十分大,则Z_{L,ext}(f_{U}-f_{L})的模可表示为
∣Z_{L,ext}(f_{U}-f_{L})∣=2πL_{e}(f_{U}-f_{L}) (4)
若电感L2与Le的值相同,那么阻抗Z_{L,ext}(f_{U}-f_{L})将是Z_{L,ext}(2f_{U})的二分之一。最终,需求匹配的优化基波阻抗为
jX_{opt}(ω)=[jωL_{2}+1/(jωC_{2})]// jωL_{e}// jωC_{ds} (5)
其间ω_{L}≤ω≤ω_{U},假如滤除二次谐波和包络的LC谐振回路在基波频率处的阻抗十分小,则在实践中难以将这个优化基波阻抗匹配到实践的负载阻抗,故匹配的难度将约束L2、Le和C2的取值。依据要求,能够得到滤除二次谐波和包络的LC谐振回路的最小阻抗值。因而,在规划短路网络的时分,应留意使滤除二次谐波和包络的LC谐振回路在基波频率处的阻抗要大于这个最小值。
4、 某军用集群体系基站下降功放回忆效应的完成
军用集群体系所用的频率规模一般为400~420MHz,其基站的功率放大器一般运用封装后的晶体管,故实践中不得不考虑封装引脚的电感效应。当和外部匹配电路合作运用时,封装引脚的寄生电感具有改进晶体管的稳定性、添加有用带宽的长处。以MRF5P21180HR6 LDMOSFET为例,这种晶体管由两个90W的功率单元构成,能到达180W的功率峰值。封装后单个功率单元的等效电路如图3所示。
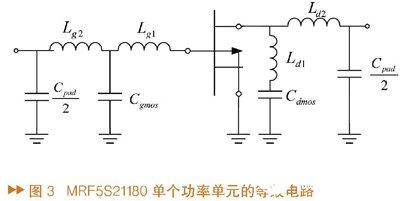
在包络这种低频下,小电容的阻抗十分大,并联结构中可疏忽不计。则针对包络重量的阻抗和频率ω、Lg1、Lg2和Ld2有联系,并可求出阻抗Z_{S,ext}(f_{U}-f_{L})和Z_{l,ext}(f_{U}-f_{L})的表达式:
∣Z_{S,ext}(f_{U}-f_{L})∣=2π(L_{g1}+L_{g2}+L_{e})(f_{U}-f_{L}) (6)
∣Z_{S,ext}(f_{U}-f_{L})∣=2π(L_{d2}+L_{e})(f_{U}-f_{L}) (7)
另一方面,关于二次谐波重量,栅极和漏极外相应的阻抗Z‘_{S,ext}(ω=2ω_{1}≈2ω_{2})和Z’_{L,ext}(ω=2ω_{1}≈2ω_{2})的表达式为,
Z‘_{S,ext}(ω=2ω_{1}≈2ω_{2})=-﹛1/jωC_{pad}/2)//[jωL_{g2}+ (jωL_{g1}//1/jωC_{g,mos})]﹜(8)
Z’_{L,ext}(ω=2ω_{1}≈2ω_{2})=?[1/(jωC_{pad}/2)//jωL_{d2} (9)
等式(8)、(9)很容易用包括串联LC谐振回路的匹配电路完成,这是因为二次谐波重量的相对带宽要比包络重量的相对带宽窄得多,故滤除包络重量比滤除二次谐波重量的难度更大。因而,包络重量对回忆效应的效果要比二次谐波重量更大。在实践使用中,因为包络重量对功率放大器的回忆效应起首要效果,故一般只对滤除包络重量的辅佐电路进行优化,高频下可用某些寄生参数较强的大电容(如钽电容)来替代滤除包络重量的串联LeCe谐振回路。
责任编辑:gt