1 导言
盲源别离(Blind Source Separation, BSS)问题是20世纪80年代提出的[1],Jutten在90年代初给出严厉的数学描绘[2]。其真正被注重仅仅近10年的事。盲源别离的研讨涉及到人工神经网络、核算信号处理和信息论的有关常识,现在已成为人工神经网络的重要开展方向之一[3]。盲源别离的开拓性研讨起源于Jutten与Herault于1991年的论文[2]。P. Comon首要提出了盲源别离的独立重量剖析(Independent Component Analysis,ICA)办法[4]。A. J. Bell和T. J. Sejnowsk在盲源别离算法的开展史上作出了重要贡献,带动了后续的研讨工作[5]。国内关于盲源别离的研讨最早始于1997年[6],首要会集在电信传输信号的盲辨认上。
盲源别离首要分为线性混叠和非线性混叠两种[7]。非线性混叠的首要有经过对线性模型的扩展和用自组织特征映射的办法[8]。
关于振荡信号的盲别离,从2000年才开端受到注重[9],并且研讨的规模首要在旋转机械和毛病诊断中。
2 盲源别离基本概念
盲源别离问题可用如下的混合方程来描绘[4]:
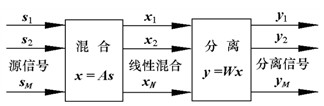
图1 线性盲源信号别离框图
事实上,在盲的领域里,人们不可能完成源信号的彻底康复。盲源信号别离的求解成果有两个不确定性:别离后信号向量的摆放方位能够改变、信号的幅值与初始相位能够改变。很显着,这样的不确定性对源信号的别离不会有任何本质的影响。
3 振荡信号盲别离的常用算法
3.1 最大似然原则算法
最大似然估量是要找到矩阵W使得所估量的输出y的概率密度函数(PDF)与假定的源信号的%&&&&&%尽可能挨近,是一种非常遍及的估量办法。
3.2 最小互信息原则及其算法
根据信息理论的最小化互信息的基本思想是挑选别离矩阵W, 使输出y的各重量之间的互依赖性最小化,在抱负状况下趋于零。
3.3 根据高阶累积量的办法
Cardoso提出了使用四阶矩进行盲信号别离的办法。在这个根底上,人们从衡量的非高斯性动身,得到快速的定点盲源抽取算法。别的Tong和Liu经过正交变换,对观测到的混迭信号的四阶矩进行奇异值分解(SVD),得到一类扩展的四阶盲辨识和多不知道信号提取算法。Cardoso还提出了根据四阶累积量的联合对角化。独立成份剖析办法中的峭度与负熵也是根据高阶累积量的盲源别离办法。
3.4 非线性混叠盲源别离
大多数的盲源别离算法都假定混叠模型是线性的,更为精确的模型应当是非线性的或弱非线性的。人们针对非线性混叠模型提出了以下几种办法:(1) 根据两层感知器网络的感知器模型法[20];(2) 根据自组织特征映射的无模型办法;(3)径向基函数网络法,这种办法鲁棒性较好。
4 振荡信号盲源别离办法的讨论
4.1 估量别离矩阵的加快梯度法
在最小化互信息原则的根底上,有关研讨推导剖分出加快梯度法的核算过程,然后对转子的振荡信号进行收集并盲别离,得到了满足的成果。
在一个转子实验台上装置2个加快度计和1个涡流传感器收集信号,得到的传感器信号与别离成果的功率谱,如图2和图3所示。
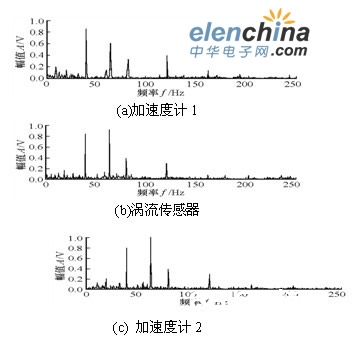
剖析标明,根据最小化互信息原理的加快梯度法能够较好地估量出别离矩阵, 其完成过程可行。
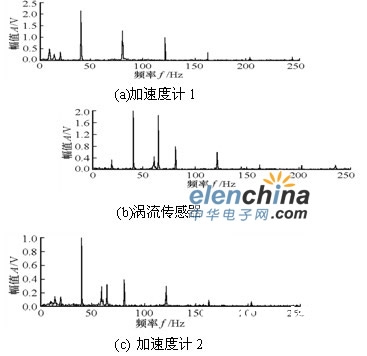
图3 别离后各传感器振荡信号的功率谱
对具有毛病的实践转子进行多传感器信号收集并进行盲别离,成果标明:收集信号中混叠的不同毛病特征能够较好地别离开来,别离后各传感器信号的功率谱图基本上只显示出一种毛病特征。可是旋转鼓励的影响不能从盲源别离的成果中彻底消除。
4.2 卷积混合盲别离时域办法
有许多文献用卷积混合矩阵模型对BSS进行了研讨。根据时域信号的盲别离[24]办法对数值信号进行卷积混合并进行盲辨认,如图4所示。混合后两个源信号别离成果阐明所用算法在低频段可给出好的别离成果,且可别离信号中的谐波信号[25]。
实践工程中的信号源个数是不明确的。可在人为设定源信号个数m的根底上,进行随机迭代,最大化各个别离信号y(n)。
对动力机械结构的不同方位上装置5个传感器,进行振荡信号收集,并对收集信号用卷积混叠矩阵进行盲别离。成果标明,挨近鼓励源的两个传感器(4、5两个传感器)得到的信号被方便地别离出来,而其他测点的传感器收集信号难以收到抱负的别离成果。这与理论办法是共同的。
第5个传感器的原始信号和别离成果如图5所示。可看出,实践的信号在时域和频域都难以直接观察出来。进行盲别离,得出两个典型的周期信号及一个随机信号。图5(b)是两个周期信号组成的频谱。两个周期信号别离是发动机、电机旋转频率[26]。实践振荡信号进行的源信号盲别离标明,所用办法在机械振荡信号盲源别离中是适用的,信号得到较好的别离。
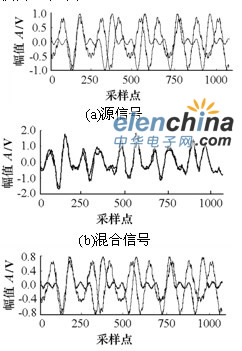
图4 两个谐波信号的别离
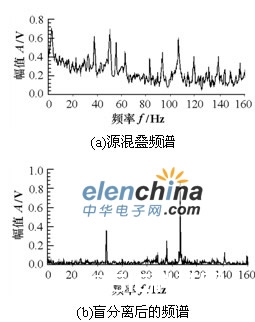
图5 实践振荡信号的盲别离
4.3 根据峭度的快速定点算法
经典的丈量非高斯办法是峭度(kurtosis)或称四阶累积量。有关研讨用根据峭度的快速定点算法对实在的转子振荡信号进行了盲源别离研讨。在转子振荡实验台上装置4个加快度传感器,三个加快度传感器是装置在轴承座上的,另一个装置在垂直于转子轴的衔接盘上以便丈量轴向的振荡状况。实验时的转速为525转/分。由此得到4个收集信号。
值得注意的是,实践收集的信号一般便是混合后的信号。所以前述数值仿真剖析办法中,“信号混合”这一步就不需求了,能够在直接对收集的信号进行预白化处理后,再用根据峭度的快速定点抽取算法进行别离。
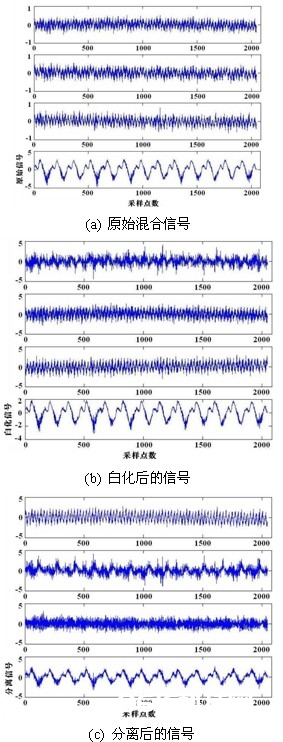
图6 转子振荡信号的盲源别离
由传感器测得的4个振荡源信号如图6(a)所示;预白化处理后的信号、别离后的信号别离如图6(b)、(c)所示。从图6(a)可看出,从原始的转子振荡信号中只能分辨出轴向冲击信号,而其他3个信号波形非常附近,无法辨认出哪个信号是哪个振荡源发生的。从图6(c)中能够明晰地别离出不同的振荡信号源。第四个信号是显着的轴向冲击信号,第二个信号是转子旋转的信号,第一个信号是轴承滚子的冲击信号,第三个信号是噪声信号。这阐明用根据峭度的快速定点算法对转子振荡信号的盲源别离是非常有用和成功的。
4.4 改进的根据Jacobi优化的极大似然估量办法
在传统的Jacobi优化算法的根底上,文献[10]探究了一种具有初始化四阶矩矩阵的优化算法,来进步算法的收敛速度和核算功率。
用6个模仿源信号进行混合,别离用FastICA算法、JADE算法来与改进Jacobi优化算法进行比较,采纳采样点数从5000改变到30000,来顺次核算各个算法的核算时刻。3种算法的核算功率如图7所示。能够看出JADE算法的核算时刻比较于其它两个算法要长,这在大采样点状况下体现更为显着,而根据初始化四阶矩矩阵的算法与FastICA算法有着挨近的核算时刻(相差3%左右)
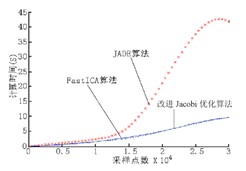
图7 三种算法的核算功率
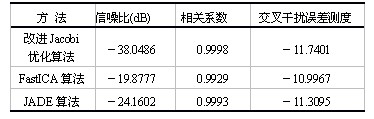
使用仿实在验来剖析各个算法别离信号的信噪比、相关系数以及穿插搅扰差错测度,如表1所示。这三个目标的值越大标明算法完成的别离信号就越迫临源信号,别离的功能就越优秀。从表1能够看出,该算法能够得到优于其它两个算法的信噪比、相关系数以及穿插搅扰差错测度。所提出的算法在别离信号的功能目标上远优于Fast%&&&&&%A算法。
4.5 鲁棒的二阶非平稳源别离办法
D. T.Pham关于一组对称正定矩阵{Mi}提出了一个不同的原则,它不需求进行任何预白化,并且对角化矩阵一起也是别离矩阵[30]。关于有不同功率谱(或等价于不同的自相关函数)的有色源,能够使用时滞协方差矩阵,并由此得到了二阶盲辨识(SOBI)算法。Choi和Cichocki对非平衡源SOBI进行修正,提出一种高效灵敏的二阶非平稳源别离(SONS)办法 [31]。
表1 各个算法别离信号的功能目标
用与4.3节相同的实验台,用SONS算法对噪声含量较少的转子体系中低转速数据进行别离,与根据负熵的快速定点算法比较,SONS算法在别离作用上的改进很小。在含有很多噪声的高速旋转状况下,根据负熵的快速定点算法对转子振荡信号的别离成果如图8(a),在改用SOBI算法后,别离成果得到了改进,如图8(b)。而在改用SONS算法,别离成果的改进则很显着,如图8(c) [32]
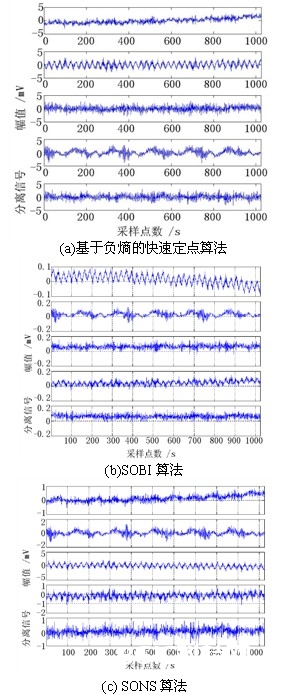
图8 用三种算法对高速数据盲源别离成果的比较
5 定论
本文介绍的内容为将盲源信号别离技能使用于机械振荡信号的毛病诊断供给了一个根据,也为盲源信号别离使用于实践工程信号的处理打下了根底。
往后应该侧重研讨的开展方向首要有3个:
(1) 怎么完成在观丈量个数源信号个数不确定或不知道时的盲别离办法研讨。
(2)更一般的非线性混叠的可别离性的研讨。
(3)对含有噪声的混叠信号进行盲别离办法的研讨。