这是《小波改换和motion信号处理》系列的第二篇,深化小波。第一篇我进行了根底常识的衬托,第三篇首要解说运用。
在上一篇中讲到,每个小波改换都会有一个mother wavelet,咱们称之为母小波,一起还有一个father wavelet,便是scaling function。而该小波的basis函数其实便是对这个母小波和父小波缩放和平移构成的。缩放倍数都是2的级数,平移的巨细和当时其缩放的程度有关。
还讲到,小波体系有许多种,不同的母小波,衍生的小波基就彻底不同。小波打开的近似方式是这样:
其间的
便是小波级数,这些级数的组合就构成了小波改换中的基basis。和傅立叶级数有一点不同的是,小波级数一般是orthonormal basis,也便是说,它们不只两两正交,还归一化了。
咱们还讲了一般小波改换的三个特色,便是小波级数是二维的,能定位时域和频域,核算很快。但咱们并没有深化解说,比方,怎样了解这个二维?它是怎样一起定位频域和时域的?
在这一篇文章里,咱们就来讨论一下这些特性背面的原理。
首要,咱们一向都在讲小波打开的近似方式。那什么是完好方式呢?之前讲到,小波basis的构成,是根据根本的小波函数,也便是母小波来做缩放和平移的。可是,母小波并非仅有的原始基。在构建小波基函数调集的时分,一般还要用到一个函数叫标准函数,scaling function,人们一般都称其为父小波。它和母小波相同,也是归一化了,并且它还需求满意一个性质,便是它和对自己自身周期平移的函数两两正交:
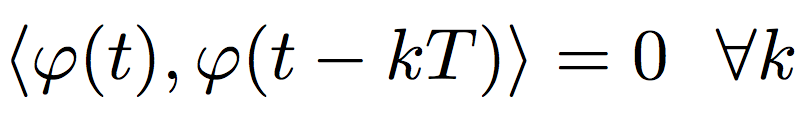
别的,为了便利处理,父小波和母小波也需求是正交的。能够说,完好的小波打开便是由母小波和父小波一起界说的。
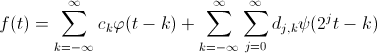
其间
是母小波,
是父小波。需求提示一点的是,这个正交朴实是为了小波剖析的便利而引进的特性,并不是说小波改换的基就必定有必要是正交的。但大部分小波改换的基确实是正交的,所以本文就直接默许正交为小波改换的首要性质之一了。引进这个父小波呢,首要是为了便利做多解析度剖析(multiresolution analysis, MRA)。说到这儿,你的问题或许会井喷了:好好的为什么出来一个父小波呢?这个scaling function是拿来干嘛的?它背面的物理含义是什么?wavelet function背面的物理含义又是什么?这个多解析度剖析又是什么呢?不急,下面,咱们环绕一个比方来稳固一下前面的常识,一起再引出新的特性。
假定咱们有这样一个信号:

该信号长度为8,是离散的一维信号。咱们要考虑的,便是怎样用小波将其打开。为了便利解说,咱们考虑最简略的一种小波,哈尔小波。下面是它的一种母小波:

那怎样构建根据这个母小波的基呢?方才说到了,要缩放,要平移。咱们先试试缩放,那便是ψ(2n):

但这样的话,它与自己的内积就不是1了,不符合小波基orthonormal的要求,所以咱们要在前面加一个系数根号二,这样咱们就得到了另一个哈尔小波的basis function:

同理,咱们能够一向这样推行下去做scale,得到4n,8n,…….下的basis function。当然在这个比方里,咱们信号长度便是8,所以做到4n就够了。但推行来说,便是这种scaling对母小波的作用为
,这是归一化后的表明方式。
平移的话也很简略,咱们能够对母小波进行平移,也能够对scale之后的basis function进行平移。比方对上一幅图中的basis function进行平移,就成了
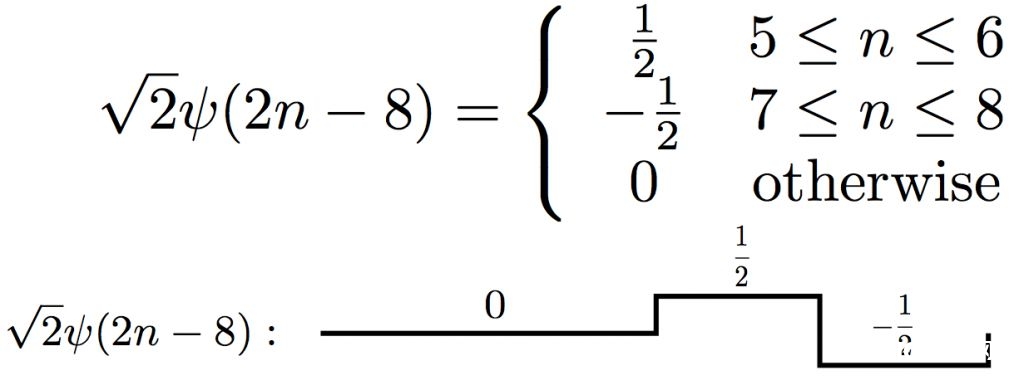
看得出来,平移后的basis function和母小波以及仅仅scale过的小波,都是正交的,附合小波basis的特色。假如咱们用ψ(n)来表明这个mother wavelet,那么这些orthonormal basis函数能够写成:
这儿的k是能够当作时域的参数,由于它操控着小波基时域的搬运,而j是频域的参数,由于它决议了小波基的频率特性。看到这儿,你应该会感觉很熟悉,由于这儿的平移和改换实质和方才对scaling function的平移改换是一模相同的。
这样,咱们就有了针对此信号space的哈尔小波basis组合:
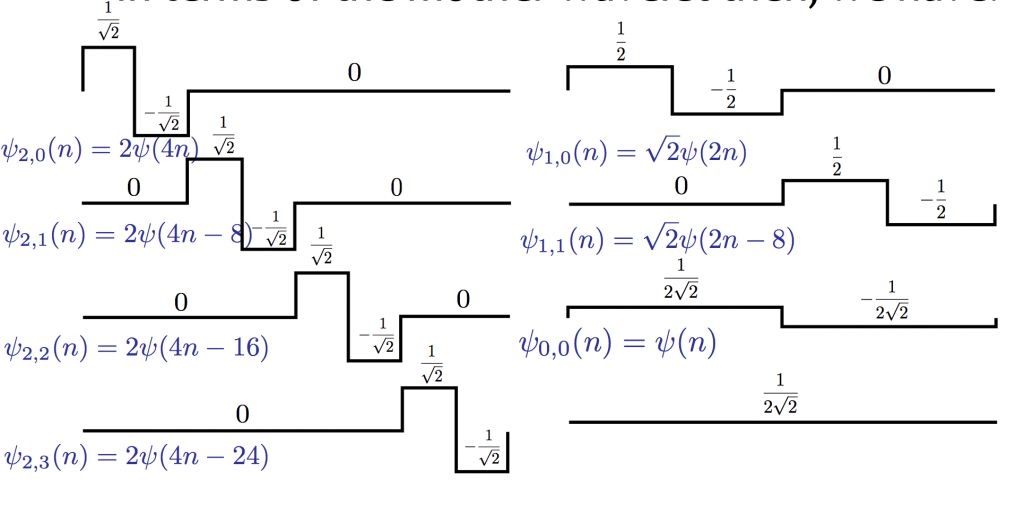
图1
能够看出,咱们用到了三层频率标准的小波函数,每往下一层,小波的数量都是上面一层的两倍。在图中,每一个小波基函数的表达方式都写在了波形的下面。
等等,你或许现已发现了,有问题。这儿为什么多了个没有函数表达式的波形呢?这货显着不是wavelet function阿。没错,它是之前说到的scaling function,也便是父小波。然后你或许就会问,为啥这个随便插了一个scaling function出来呢?分明方针信号现已能够用纯的小波基组合表明了。是,确实是,就算不包括scaling function,这些小波函数自身也组成了正交归一基,但假如仅限于此的话,小波改换也就没那么奇特的成效了。引进这个scaling function,才干引进咱们说到的多解析度剖析的理论,而小波改换的强壮,就体现在这个多解析度上。那在这儿,咱们怎样用这个多解析度呢?这个哈尔小波basis组合是怎样经过多解析度推导出来的呢?
话说在数学界说中,有一种空间叫Lebesgue空间,关于信号处理非常重要,能够用L^p(R)表明,指的是由p次可积函数所组成的函数空间。咱们在小波改换中要研讨的信号都是归于L^2(R)空间的,这个空间是R上的一切处处平方可积的可测函数的调集,这样就等于对信号提出了一个约束,便是信号能量有必要是有限的,不然它就不行积了。小波改换的界说都是根据但不限于L^2(R)中的信号的。这玩意的特性要详细解说起来太数学了,牵涉到太多泛函常识,我就不在这儿胪陈了。并且老实说我也没才能彻底讲清楚,究竟不是学这个的,有爱好能够参阅wiki。总归你记住,小波改换研讨中所运用的信号根本都是平方可积的信号,但其运用不限于这种信号,就行了。
对L^2(R)空间做MRA是在干嘛呢?便是说,在L^2(R)空间中,咱们能够找出一个嵌套的空间序列
,并有下列性质:
(i)
(ii)
(iii)
(iv)
(v) 有这样一个方程
,
是
的orthonormal basis。
我来简略解说一下这些性质。这个V_j都是L^2(R)空间中的子空间,然后他们是由小到大的,交集是{0},由于这是最小的子空间,并集便是L空间。是不是有点难以了解?不要紧,看看下面这个图就清楚了:

这个图是圈骗局圈圈,最里边的圈是V0,之后分别是V1,V2,V3,V4 。那他们风趣的性质便是,假如有一个函数f(t)他归于一个某空间,那你将其在时域上平移,它仍是归于这个空间。但假如你对它频域的扩大或缩小,它就会相应移到下一个或许上一个空间了。
一起咱们还知道,你要描述每一个空间的话,都需求有对应的orthonormal basis,这是必定的,那关于V0来讲,它的orthonormal basis便是
这一系列函数是什么呢?是
的时域改换,并且咱们方才也说了,时域上平移,是不会跳出这个空间的。这样,咱们就能够说,由这一系列basis所界说的L^2(R)子空间V0被这些basis所span,表明成:
k从负无量到正无量。上面的bar表明这是一个闭包空间,也便是说

这样,咱们就界说了根本的V0这个子空间。方才说了,这个子空间的基都是对
的整数时域改换,这儿咱们称
为scaling function,所以换个说法,便是说这儿整个子空间V0,由scaling function和其时域改换的兄弟们span。
当然,假如这个scaling function仅仅用来代表一个子空间的,那它的位置也就不会这么重要了。方才咱们说到,这个嵌套空间序列有一个性质,
。这便是这个函数,假如你对它频域的扩大或缩小,它就会相应移到下一个或许上一个空间了。这个性质就有意思了,它代表什么呢?关于任何一个包括V0的更上一层的空间来讲,他们的基都能够经过对scaling function做频域的scale后再做时域上的整数改换得到!推行开来便是说,当
咱们有
这也就意味着,关于任何归于V_j空间的函数f(t),都能够表明为:
到这儿,咱们就理解这些个子空间和那个随便冒出来的scaling function的作用了。scaling的构建这些不同的子空间的根底,当j越大的时分,每一次你对频率改换后的scaling function所做的时域上的整数平移起伏会越小,这样在这个j子空间里边得到的f(t)表明粒度会很细,细节展示许多。反之亦然。浅显点说,便是对scaling function的改换平移给你不同的子空间,而不同的子空间给你不同的分辨率,这样你就能够用不同的分辨率去看方针信号。
下面便是时分看看什么是MRA equation了,这是愈加风趣,也是愈加中心的当地。经过方才的解说,V0归于V1,那scaling function
是在V0中的,天然也在V1中了。咱们把他写成V1的基的线性组合,那便是
其间的h(n)是scaling function的系数,也叫做scaling filter或许scaling vector,能够是实数,也能够是虚数。根号2是为了保持norm为1的。看,在这个公式里,咱们就把归于V0的函数用V1的基表明出来了。同理